
In physics and chemistry, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars.
In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.
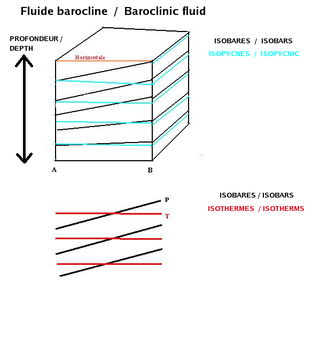
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure. A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.

Terminal velocity is the maximum speed attainable by an object as it falls through a fluid. It is reached when the sum of the drag force (Fd) and the buoyancy is equal to the downward force of gravity (FG) acting on the object. Since the net force on the object is zero, the object has zero acceleration. For objects falling through air at normal pressure, the buoyant force is usually dismissed and not taken into account, as its effects are negligible.
In viscous fluid dynamics, the Archimedes number (Ar), is a dimensionless number used to determine the motion of fluids due to density differences, named after the ancient Greek scientist and mathematician Archimedes.
In fluid dynamics, the Boussinesq approximation is used in the field of buoyancy-driven flow. It ignores density differences except where they appear in terms multiplied by g, the acceleration due to gravity. The essence of the Boussinesq approximation is that the difference in inertia is negligible but gravity is sufficiently strong to make the specific weight appreciably different between the two fluids. The existence of Sound waves in a Boussinesq fluid is not possible as sound is the result of density fluctuations within a fluid.

The Rankine–Hugoniot conditions, also referred to as Rankine–Hugoniot jump conditions or Rankine–Hugoniot relations, describe the relationship between the states on both sides of a shock wave or a combustion wave in a one-dimensional flow in fluids or a one-dimensional deformation in solids. They are named in recognition of the work carried out by Scottish engineer and physicist William John Macquorn Rankine and French engineer Pierre Henri Hugoniot.
In fluid mechanics, or more generally continuum mechanics, incompressible flow refers to a flow in which the material density of each fluid parcel — an infinitesimal volume that moves with the flow velocity — is time-invariant. An equivalent statement that implies incompressible flow is that the divergence of the flow velocity is zero.

Internal waves are gravity waves that oscillate within a fluid medium, rather than on its surface. To exist, the fluid must be stratified: the density must change with depth/height due to changes, for example, in temperature and/or salinity. If the density changes over a small vertical distance, the waves propagate horizontally like surface waves, but do so at slower speeds as determined by the density difference of the fluid below and above the interface. If the density changes continuously, the waves can propagate vertically as well as horizontally through the fluid.
The virial expansion is a model of thermodynamic equations of state. It expresses the pressure P of a gas in local equilibrium as a power series of the density. This equation may be represented in terms of the compressibility factor, Z, as This equation was first proposed by Kamerlingh Onnes. The terms A, B, and C represent the virial coefficients. The leading coefficient A is defined as the constant value of 1, which ensures that the equation reduces to the ideal gas expression as the gas density approaches zero.

The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.
In atmospheric dynamics, oceanography, asteroseismology and geophysics, the Brunt–Väisälä frequency, or buoyancy frequency, is a measure of the stability of a fluid to vertical displacements such as those caused by convection. More precisely it is the frequency at which a vertically displaced parcel will oscillate within a statically stable environment. It is named after David Brunt and Vilho Väisälä. It can be used as a measure of atmospheric stratification.

The Chapman–Jouguet condition holds approximately in detonation waves in high explosives. It states that the detonation propagates at a velocity at which the reacting gases just reach sonic velocity as the reaction ceases.
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis, especially along the polar front, and in analyzing flow in the ocean.

Double diffusive convection is a fluid dynamics phenomenon that describes a form of convection driven by two different density gradients, which have different rates of diffusion.

A bubble column reactor is a chemical reactor that belongs to the general class of multiphase reactors, which consists of three main categories: trickle bed reactor, fluidized bed reactor, and bubble column reactor. A bubble column reactor is a very simple device consisting of a vertical vessel filled with water with a gas distributor at the inlet. Due to the ease of design and operation, which does not involve moving parts, they are widely used in the chemical, biochemical, petrochemical, and pharmaceutical industries to generate and control gas-liquid chemical reactions.
The Taylor–Goldstein equation is an ordinary differential equation used in the fields of geophysical fluid dynamics, and more generally in fluid dynamics, in presence of quasi-2D flows. It describes the dynamics of the Kelvin–Helmholtz instability, subject to buoyancy forces, for stably stratified fluids in the dissipation-less limit. Or, more generally, the dynamics of internal waves in the presence of a (continuous) density stratification and shear flow. The Taylor–Goldstein equation is derived from the 2D Euler equations, using the Boussinesq approximation.
Flotation of flexible objects is a phenomenon in which the bending of a flexible material allows an object to displace a greater amount of fluid than if it were completely rigid. This ability to displace more fluid translates directly into an ability to support greater loads, giving the flexible structure an advantage over a similarly rigid one. Inspiration to study the effects of elasticity are taken from nature, where plants, such as black pepper, and animals living at the water surface have evolved to take advantage of the load-bearing benefits elasticity imparts.
The density ratio of a column of seawater is a measure of the relative contributions of temperature and salinity in determining the density gradient. At a density ratio of 1, temperature and salinity are said to be compensated: their density signatures cancel, leaving a density gradient of zero. The formula for the density ratio, , is:
The shear viscosity of a fluid is a material property that describes the friction between internal neighboring fluid surfaces flowing with different fluid velocities. This friction is the effect of (linear) momentum exchange caused by molecules with sufficient energy to move between these fluid sheets due to fluctuations in their motion. The viscosity is not a material constant, but a material property that depends on temperature, pressure, fluid mixture composition, local velocity variations. This functional relationship is described by a mathematical viscosity model called a constitutive equation which is usually far more complex than the defining equation of shear viscosity. One such complicating feature is the relation between the viscosity model for a pure fluid and the model for a fluid mixture which is called mixing rules. When scientists and engineers use new arguments or theories to develop a new viscosity model, instead of improving the reigning model, it may lead to the first model in a new class of models. This article will display one or two representative models for different classes of viscosity models, and these classes are:

















