See also
| This disambiguation page lists articles associated with the title Stress tensor. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
Stress tensor may refer to:
| This disambiguation page lists articles associated with the title Stress tensor. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
Mechanics is the area of physics concerned with the motions of macroscopic objects. Forces applied to objects result in displacements, or changes of an object's position relative to its environment. This branch of physics has its origins in Ancient Greece with the writings of Aristotle and Archimedes. During the early modern period, scientists such as Galileo, Kepler, and Newton laid the foundation for what is now known as classical mechanics. It is a branch of classical physics that deals with particles that are either at rest or are moving with velocities significantly less than the speed of light. It can also be defined as a branch of science which deals with the motion of and forces on bodies not in the quantum realm. The field is today less widely understood in terms of quantum theory.

The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. This density and flux of energy and momentum are the sources of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity.
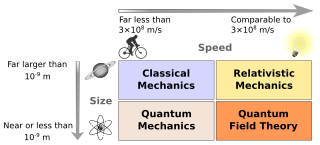
Classical physics refers to theories of physics that predate modern, more complete, or more widely applicable theories. If a currently accepted theory is considered to be modern, and its introduction represented a major paradigm shift, then the previous theories, or new theories based on the older paradigm, will often be referred to as belonging to the realm of "classical physics".
In the special theory of relativity, four-force is a four-vector that replaces the classical force.
In science and especially in mathematical studies, a variational principle is one that enables a problem to be solved using the calculus of variations, which concerns the finding functions which optimizes the value of quantities that depend upon those functions. For example, the answer to the question asking for thee shape of a hanging chain suspended at both ends—a catenery—can be solved using a variational principle. In particular, the solution is the function that minimizes the gravitational potential energy of the chain.
Since the 19th century, some physicists, notably Albert Einstein, have attempted to develop a single theoretical framework that can account for all the fundamental forces of nature – a unified field theory. Classical unified field theories are attempts to create a unified field theory based on classical physics. In particular, unification of gravitation and electromagnetism was actively pursued by several physicists and mathematicians in the years between the two World Wars. This work spurred the purely mathematical development of differential geometry.
In fluid mechanics and astrophysics, the relativistic Euler equations are a generalization of the Euler equations that account for the effects of general relativity.They have applications in high-energy astrophysics and numerical relativity, where they are commonly used for describing phenomena such as gamma-ray bursts, accretion phenomena, and neutron stars, often with the addition of a magnetic field. Note: for consistency with the literature, this article makes use of natural units, namely the speed of lightand the Einstein summation convention.
In theoretical physics and applied mathematics, a field equation is a partial differential equation which determines the dynamics of a physical field, specifically the time evolution and spatial distribution of the field. The solutions to the equation are mathematical functions which correspond directly to the field, as functions of time and space. Since the field equation is a partial differential equation, there are families of solutions which represent a variety of physical possibilities. Usually, there is not just a single equation, but a set of coupled equations which must be solved simultaneously. Field equations are not ordinary differential equations since a field depends on space and time, which requires at least two variables.
In mathematical physics, a null dust solution is a Lorentzian manifold in which the Einstein tensor is null. Such a spacetime can be interpreted as an exact solution of Einstein's field equation, in which the only mass-energy present in the spacetime is due to some kind of massless radiation.
In physics, relativistic mechanics refers to mechanics compatible with special relativity (SR) and general relativity (GR). It provides a non-quantum mechanical description of a system of particles, or of a fluid, in cases where the velocities of moving objects are comparable to the speed of light c. As a result, classical mechanics is extended correctly to particles traveling at high velocities and energies, and provides a consistent inclusion of electromagnetism with the mechanics of particles. This was not possible in Galilean relativity, where it would be permitted for particles and light to travel at any speed, including faster than light. The foundations of relativistic mechanics are the postulates of special relativity and general relativity. The unification of SR with quantum mechanics is relativistic quantum mechanics, while attempts for that of GR is quantum gravity, an unsolved problem in physics.
In mathematics, mathematical physics, and theoretical physics, the spin tensor is a quantity used to describe the rotational motion of particles in spacetime. The tensor has application in general relativity and special relativity, as well as quantum mechanics, relativistic quantum mechanics, and quantum field theory.
Scalar theories of gravitation are field theories of gravitation in which the gravitational field is described using a scalar field, which is required to satisfy some field equation.
A scalar or scalar quantity in physics is a physical quantity that can be described by a single element of a number field such as a real number, often accompanied by units of measurement. A scalar is usually said to be a physical quantity that only has magnitude, possibly a sign, and no other characteristics. This is in contrast to vectors, tensors, etc. which are described by several numbers that characterize their magnitude, direction, and so on.
Asım Orhan Barut was a Turkish-American theoretical physicist.

In relativistic physics, the electromagnetic stress–energy tensor is the contribution to the stress–energy tensor due to the electromagnetic field. The stress–energy tensor describes the flow of energy and momentum in spacetime. The electromagnetic stress–energy tensor contains the negative of the classical Maxwell stress tensor that governs the electromagnetic interactions.
Electromagnetic mass was initially a concept of classical mechanics, denoting as to how much the electromagnetic field, or the self-energy, is contributing to the mass of charged particles. It was first derived by J. J. Thomson in 1881 and was for some time also considered as a dynamical explanation of inertial mass per se. Today, the relation of mass, momentum, velocity, and all forms of energy – including electromagnetic energy – is analyzed on the basis of Albert Einstein's special relativity and mass–energy equivalence. As to the cause of mass of elementary particles, the Higgs mechanism in the framework of the relativistic Standard Model is currently used. In addition, some problems concerning the electromagnetic mass and self-energy of charged particles are still studied.
This article will use the Einstein summation convention.
In physics, relativistic quantum mechanics (RQM) is any Poincaré covariant formulation of quantum mechanics (QM). This theory is applicable to massive particles propagating at all velocities up to those comparable to the speed of light c, and can accommodate massless particles. The theory has application in high energy physics, particle physics and accelerator physics, as well as atomic physics, chemistry and condensed matter physics. Non-relativistic quantum mechanics refers to the mathematical formulation of quantum mechanics applied in the context of Galilean relativity, more specifically quantizing the equations of classical mechanics by replacing dynamical variables by operators. Relativistic quantum mechanics (RQM) is quantum mechanics applied with special relativity. Although the earlier formulations, like the Schrödinger picture and Heisenberg picture were originally formulated in a non-relativistic background, a few of them also work with special relativity.

Classical mechanics describes the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars and galaxies.

In physics, a field is a physical quantity, represented by a number or tensor, that has a value for each point in space-time. For example, on a weather map, the surface temperature is described by assigning a real number to each point on a map; the temperature can be considered at a fixed point in time or over some time interval, to study the dynamics of temperature change. A surface wind map, assigning a vector to each point on a map that describes the wind velocity at that point, would be an example of a 1-dimensional tensor field, i.e. a vector field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, and the full description of electrodynamics can be formulated in terms of two interacting vector fields at each point in space-time, or as a single-rank 2-tensor field theory.