In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.

In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to group theory, which makes them simpler and easier to understand.

In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is an integer factorization of 15, and (x – 2)(x + 2) is a polynomial factorization of x2 – 4.
In numerical analysis, a root-finding algorithm is an algorithm for finding zeros, also called "roots", of continuous functions. A zero of a function f is a number x such that f(x) = 0. As, generally, the zeros of a function cannot be computed exactly nor expressed in closed form, root-finding algorithms provide approximations to zeros. For functions from the real numbers to real numbers or from the complex numbers to the complex numbers, these are expressed either as floating-point numbers without error bounds or as floating-point values together with error bounds. The latter, approximations with error bounds, are equivalent to small isolating intervals for real roots or disks for complex roots.

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.
In mathematics, an nth root of a number x is a number r which, when raised to the power of the positive integer n, yields x:
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.
In mathematics, an algebraic equation or polynomial equation is an equation of the form , where P is a polynomial with coefficients in some field, often the field of the rational numbers. For example, is an algebraic equation with integer coefficients and
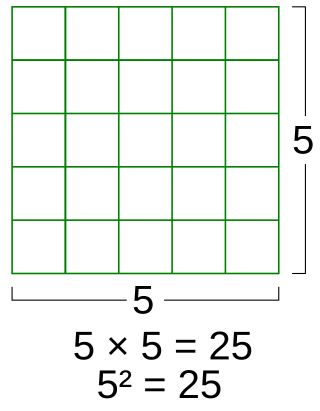
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x2. The adjective which corresponds to squaring is quadratic.
In mathematics, the Sturm sequence of a univariate polynomial p is a sequence of polynomials associated with p and its derivative by a variant of Euclid's algorithm for polynomials. Sturm's theorem expresses the number of distinct real roots of p located in an interval in terms of the number of changes of signs of the values of the Sturm sequence at the bounds of the interval. Applied to the interval of all the real numbers, it gives the total number of real roots of p.
In mathematics, the resultant of two polynomials is a polynomial expression of their coefficients that is equal to zero if and only if the polynomials have a common root, or, equivalently, a common factor. In some older texts, the resultant is also called the eliminant.

In mathematics, Puiseux series are a generalization of power series that allow for negative and fractional exponents of the indeterminate. For example, the series
In mathematics and computer algebra, factorization of polynomials or polynomial factorization expresses a polynomial with coefficients in a given field or in the integers as the product of irreducible factors with coefficients in the same domain. Polynomial factorization is one of the fundamental components of computer algebra systems.
In mathematics, a univariate polynomial of degree n with real or complex coefficients has n complex roots, if counted with their multiplicities. They form a multiset of n points in the complex plane. This article concerns the geometry of these points, that is the information about their localization in the complex plane that can be deduced from the degree and the coefficients of the polynomial.
In algebra, the greatest common divisor of two polynomials is a polynomial, of the highest possible degree, that is a factor of both the two original polynomials. This concept is analogous to the greatest common divisor of two integers.
A system of polynomial equations is a set of simultaneous equations f1 = 0, ..., fh = 0 where the fi are polynomials in several variables, say x1, ..., xn, over some field k.
In mathematics, and, more specifically in numerical analysis and computer algebra, real-root isolation of a polynomial consist of producing disjoint intervals of the real line, which contain each one real root of the polynomial, and, together, contain all the real roots of the polynomial.
Finding polynomial roots is a long-standing problem that has been the object of much research throughout history. A testament to this is that up until the 19th century, algebra meant essentially theory of polynomial equations.
The square-root sum problem (SRS) is a computational decision problem from the field of numerical analysis, with applications to computational geometry.







