
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics, numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and biology.

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
Computational science, also known as scientific computing, technical computing or scientific computation (SC), is a division of science that uses advanced computing capabilities to understand and solve complex physical problems. This includes
Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations, including fluid mechanics, acoustics, electromagnetics, fracture mechanics, and contact mechanics.
In numerical analysis, a multigrid method is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners.

Finite-difference time-domain (FDTD) or Yee's method is a numerical analysis technique used for modeling computational electrodynamics. Since it is a time-domain method, FDTD solutions can cover a wide frequency range with a single simulation run, and treat nonlinear material properties in a natural way.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. A typical goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.

Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers.
Computational mechanics is the discipline concerned with the use of computational methods to study phenomena governed by the principles of mechanics. Before the emergence of computational science as a "third way" besides theoretical and experimental sciences, computational mechanics was widely considered to be a sub-discipline of applied mechanics. It is now considered to be a sub-discipline within computational science.
Dassault Systèmes Simulia Corp. is a computer-aided engineering (CAE) vendor. Formerly known as Abaqus Inc. and previously Hibbitt, Karlsson & Sorensen, Inc., (HKS), the company was founded in 1978 by David Hibbitt, Bengt Karlsson and Paul Sorensen, and has its headquarters in Providence, Rhode Island.

In the field of numerical analysis, meshfree methods are those that do not require connection between nodes of the simulation domain, i.e. a mesh, but are rather based on interaction of each node with all its neighbors. As a consequence, original extensive properties such as mass or kinetic energy are no longer assigned to mesh elements but rather to the single nodes. Meshfree methods enable the simulation of some otherwise difficult types of problems, at the cost of extra computing time and programming effort. The absence of a mesh allows Lagrangian simulations, in which the nodes can move according to the velocity field.
The finite-difference frequency-domain (FDFD) method is a numerical solution method for problems usually in electromagnetism and sometimes in acoustics, based on finite-difference approximations of the derivative operators in the differential equation being solved.
In mathematics, the Trefftz method is a method for the numerical solution of partial differential equations named after the German mathematician Erich Trefftz(de) (1888–1937). It falls within the class of finite element methods.

The Finite Element Machine (FEM) was a late 1970s-early 1980s NASA project to build and evaluate the performance of a parallel computer for structural analysis. The FEM was completed and successfully tested at the NASA Langley Research Center in Hampton, Virginia. The motivation for FEM arose from the merger of two concepts: the finite element method of structural analysis and the introduction of relatively low-cost microprocessors.
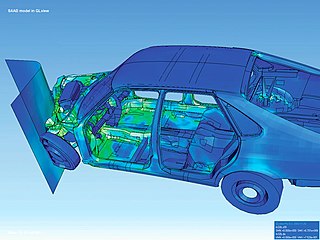
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.
hp-FEM is a generalization of the finite element method (FEM) for solving partial differential equations numerically based on piecewise-polynomial approximations. hp-FEM originates from the discovery by Barna A. Szabó and Ivo Babuška that the finite element method converges exponentially fast when the mesh is refined using a suitable combination of h-refinements and p-refinements .The exponential convergence of hp-FEM has been observed by numerous independent researchers.
Smoothed finite element methods (S-FEM) are a particular class of numerical simulation algorithms for the simulation of physical phenomena. It was developed by combining meshfree methods with the finite element method. S-FEM are applicable to solid mechanics as well as fluid dynamics problems, although so far they have mainly been applied to the former.
Fluid motion is governed by the Navier–Stokes equations, a set of coupled and nonlinear partial differential equations derived from the basic laws of conservation of mass, momentum and energy. The unknowns are usually the flow velocity, the pressure and density and temperature. The analytical solution of this equation is impossible hence scientists resort to laboratory experiments in such situations. The answers delivered are, however, usually qualitatively different since dynamical and geometric similitude are difficult to enforce simultaneously between the lab experiment and the prototype. Furthermore, the design and construction of these experiments can be difficult, particularly for stratified rotating flows. Computational fluid dynamics (CFD) is an additional tool in the arsenal of scientists. In its early days CFD was often controversial, as it involved additional approximation to the governing equations and raised additional (legitimate) issues. Nowadays CFD is an established discipline alongside theoretical and experimental methods. This position is in large part due to the exponential growth of computer power which has allowed us to tackle ever larger and more complex problems.
The finite point method (FPM) is a meshfree method for solving partial differential equations (PDEs) on scattered distributions of points. The FPM was proposed in the mid-nineties in, and with the purpose to facilitate the solution of problems involving complex geometries, free surfaces, moving boundaries and adaptive refinement. Since then, the FPM has evolved considerably, showing satisfactory accuracy and capabilities to deal with different fluid and solid mechanics problems.







