
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known.

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle in physics, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves.
In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state that has dynamics most closely resembling the oscillatory behavior of a classical harmonic oscillator. It was the first example of quantum dynamics when Erwin Schrödinger derived it in 1926, while searching for solutions of the Schrödinger equation that satisfy the correspondence principle. The quantum harmonic oscillator arise in the quantum theory of a wide range of physical systems. For instance, a coherent state describes the oscillating motion of a particle confined in a quadratic potential well. The coherent state describes a state in a system for which the ground-state wavepacket is displaced from the origin of the system. This state can be related to classical solutions by a particle oscillating with an amplitude equivalent to the displacement.
Creation operators and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one. A creation operator increases the number of particles in a given state by one, and it is the adjoint of the annihilation operator. In many subfields of physics and chemistry, the use of these operators instead of wavefunctions is known as second quantization. They were introduced by Paul Dirac.

In quantum mechanics, a two-state system is a quantum system that can exist in any quantum superposition of two independent quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.
Quantum noise is noise arising from the indeterminate state of matter in accordance with fundamental principles of quantum mechanics, specifically the uncertainty principle and via zero-point energy fluctuations. Quantum noise is due to the apparently discrete nature of the small quantum constituents such as electrons, as well as the discrete nature of quantum effects, such as photocurrents.
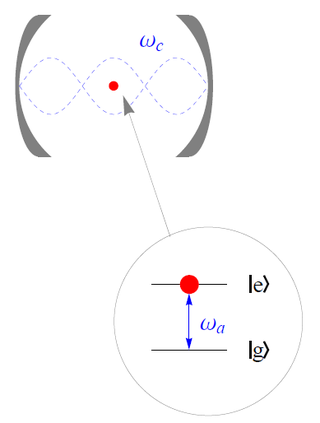
The Jaynes–Cummings model is a theoretical model in quantum optics. It describes the system of a two-level atom interacting with a quantized mode of an optical cavity, with or without the presence of light. It was originally developed to study the interaction of atoms with the quantized electromagnetic field in order to investigate the phenomena of spontaneous emission and absorption of photons in a cavity.
In quantum mechanics, the energies of cyclotron orbits of charged particles in a uniform magnetic field are quantized to discrete values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau.
Resonance fluorescence is the process in which a two-level atom system interacts with the quantum electromagnetic field if the field is driven at a frequency near to the natural frequency of the atom.
A vacuum Rabi oscillation is a damped oscillation of an initially excited atom coupled to an electromagnetic resonator or cavity in which the atom alternately emits photon(s) into a single-mode electromagnetic cavity and reabsorbs them. The atom interacts with a single-mode field confined to a limited volume V in an optical cavity. Spontaneous emission is a consequence of coupling between the atom and the vacuum fluctuations of the cavity field.
The Mattis–Bardeen theory is a theory that describes the electrodynamic properties of superconductivity. It is commonly applied in the research field of optical spectroscopy on superconductors.
An LC circuit can be quantized using the same methods as for the quantum harmonic oscillator. An LC circuit is a variety of resonant circuit, and consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C. When connected together, an electric current can alternate between them at the circuit's resonant frequency:
An electric dipole transition is the dominant effect of an interaction of an electron in an atom with the electromagnetic field.
Circuit quantum electrodynamics provides a means of studying the fundamental interaction between light and matter. As in the field of cavity quantum electrodynamics, a single photon within a single mode cavity coherently couples to a quantum object (atom). In contrast to cavity QED, the photon is stored in a one-dimensional on-chip resonator and the quantum object is no natural atom but an artificial one. These artificial atoms usually are mesoscopic devices which exhibit an atom-like energy spectrum. The field of circuit QED is a prominent example for quantum information processing and a promising candidate for future quantum computation.

Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems. In application, understanding symmetries can also provide insights on the eigenstates that can be expected. For example, the existence of degenerate states can be inferred by the presence of non commuting symmetry operators or that the non degenerate states are also eigenvectors of symmetry operators.
Ramsey interferometry, also known as the separated oscillating fields method, is a form of particle interferometry that uses the phenomenon of magnetic resonance to measure transition frequencies of particles. It was developed in 1949 by Norman Ramsey, who built upon the ideas of his mentor, Isidor Isaac Rabi, who initially developed a technique for measuring particle transition frequencies. Ramsey's method is used today in atomic clocks and in the SI definition of the second. Most precision atomic measurements, such as modern atom interferometers and quantum logic gates, have a Ramsey-type configuration. A more modern method, known as Ramsey–Bordé interferometry uses a Ramsey configuration and was developed by French physicist Christian Bordé and is known as the Ramsey–Bordé interferometer. Bordé's main idea was to use atomic recoil to create a beam splitter of different geometries for an atom-wave. The Ramsey–Bordé interferometer specifically uses two pairs of counter-propagating interaction waves, and another method named the "photon-echo" uses two co-propagating pairs of interaction waves.
In quantum mechanics, magnetic resonance is a resonant effect that can appear when a magnetic dipole is exposed to a static magnetic field and perturbed with another, oscillating electromagnetic field. Due to the static field, the dipole can assume a number of discrete energy eigenstates, depending on the value of its angular momentum (azimuthal) quantum number. The oscillating field can then make the dipole transit between its energy states with a certain probability and at a certain rate. The overall transition probability will depend on the field's frequency and the rate will depend on its amplitude. When the frequency of that field leads to the maximum possible transition probability between two states, a magnetic resonance has been achieved. In that case, the energy of the photons composing the oscillating field matches the energy difference between said states. If the dipole is tickled with a field oscillating far from resonance, it is unlikely to transition. That is analogous to other resonant effects, such as with the forced harmonic oscillator. The periodic transition between the different states is called Rabi cycle and the rate at which that happens is called Rabi frequency. The Rabi frequency should not be confused with the field's own frequency. Since many atomic nuclei species can behave as a magnetic dipole, this resonance technique is the basis of nuclear magnetic resonance, including nuclear magnetic resonance imaging and nuclear magnetic resonance spectroscopy.
In quantum computing, Mølmer–Sørensen gate scheme refers to an implementation procedure for various multi-qubit quantum logic gates used mostly in trapped ion quantum computing. This procedure is based on the original proposition by Klaus Mølmer and Anders Sørensen in 1999-2000.
The Dicke model is a fundamental model of quantum optics, which describes the interaction between light and matter. In the Dicke model, the light component is described as a single quantum mode, while the matter is described as a set of two-level systems. When the coupling between the light and matter crosses a critical value, the Dicke model shows a mean-field phase transition to a superradiant phase. This transition belongs to the Ising universality class and was realized in cavity quantum electrodynamics experiments. Although the superradiant transition bears some analogy with the lasing instability, these two transitions belong to different universality classes.







































