Symmetric power

Last updated February 26, 2019

In mathematics, the n-th symmetric power of an object X is the quotient of the n-fold product $X^{n}:=X\times \cdots \times X$ by the permutation action of the symmetric group ${\mathfrak {S}}_{n}$ .

In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group S_n defined over a finite set of n symbols consists of the permutation operations that can be performed on the n symbols. Since there are n! possible permutation operations that can be performed on a tuple composed of n symbols, it follows that the number of elements of the symmetric group S_n is n!.

More precisely, the notion exists at least in the following three areas:

In linear algebra, the n-th symmetric power of a vector space V is the vector subspace of the symmetric algebra of V consisting of degree-n elements (here the product is a tensor product).
In algebraic topology, the n-th symmetric power of a topological space X is the quotient space $X^{n}/{\mathfrak {S}}_{n}$ , as in the beginning of this article.
In algebraic geometry, a symmetric power is defined in a way similar to that in algebraic topology. For example, if $X=\operatorname {Spec} (A)$ is an affine variety, then the GIT quotient $\operatorname {Spec} ((A\otimes _{k}\dots \otimes _{k}A)^{{\mathfrak {S}}_{n}})$ is the n-th symmetric power of X.

Linear algebra is the branch of mathematics concerning linear equations such as

In mathematics, the symmetric algebraS(V) on a vector space V over a field K is the free commutative unital associative algebra over K containing V.

In mathematics, the tensor product $V \otimes W$ of two vector spaces $V$ and $W$ is itself a vector space, endowed with the operation of bilinear composition, denoted by $\otimes$ , from ordered pairs in the Cartesian product $V \times W$ onto $V \otimes W$ in a way that generalizes the outer product. The tensor product of $V$ and $W$ is the vector space generated by the symbols $v \otimes w$ , with $v \in V$ and $w \in W$ , in which the relations of bilinearity are imposed for the product operation $\otimes$ , and no other relations are assumed to hold. The tensor product space is thus the "freest" such vector space, in the sense of having the fewest constraints.

Related Research Articles

In mathematics, an associative algebra is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.

In algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by $, is the set of all prime ideals of R . It is commonly augmented with the Zariski topology and with a structure sheaf, turning it into a locally ringed space. A locally ringed space of this form is called an affine scheme .$

In mathematics, a ring is one of the fundamental algebraic structures used in abstract algebra. It consists of a set equipped with two binary operations that generalize the arithmetic operations of addition and multiplication. Through this generalization, theorems from arithmetic are extended to non-numerical objects such as polynomials, series, matrices and functions.

In commutative algebra, the Krull dimension of a commutative ring R, named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. More generally the Krull dimension can be defined for modules over possibly non-commutative rings as the deviation of the poset of submodules.

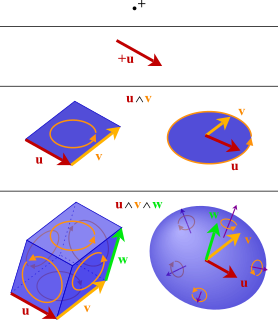
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors u and v, denoted by u ∧ v, is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of u ∧ v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. Like the cross product, the exterior product is anticommutative, meaning that u ∧ v = −(v ∧ u) for all vectors u and v, but, unlike the cross product, the exterior product is associative. One way to visualize a bivector is as a family of parallelograms all lying in the same plane, having the same area, and with the same orientation—a choice of clockwise or counterclockwise.

In algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those operations defined for the integers. Ring theory studies the structure of rings, their representations, or, in different language, modules, special classes of rings, as well as an array of properties that proved to be of interest both within the theory itself and for its applications, such as homological properties and polynomial identities.

Lie algebra representation homomorphism of Lie algebras whose codomain is the endomorphism algebra of a vector space

In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator. In the language of physics, one looks for a vector space $together with a collection of operators on satisfying some fixed set of commutation relations, such as the relations satisfied by the angular momentum operators.$

In mathematics, a universal enveloping algebra is the most general algebra that contains all representations of a Lie algebra.

In mathematics the spin group Spin(n) is the double cover of the special orthogonal group SO(n) = SO(n, R), such that there exists a short exact sequence of Lie groups

In mathematics, the Chern–Weil homomorphism is a basic construction in Chern–Weil theory that computes topological invariants of vector bundles and principal bundles on a smooth manifold M in terms of connections and curvature representing classes in the de Rham cohomology rings of M. That is, the theory forms a bridge between the areas of algebraic topology and differential geometry. It was developed in the late 1940s by Shiing-Shen Chern and André Weil, in the wake of proofs of the generalized Gauss–Bonnet theorem. This theory was an important step in the theory of characteristic classes.

In differential geometry, a Lie algebra-valued form is a differential form with values in a Lie algebra. Such forms have important applications in the theory of connections on a principal bundle as well as in the theory of Cartan connections.

In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps. The module construction is analogous to the construction of the tensor product of vector spaces, but can be carried out for a pair of modules over a commutative ring resulting in a third module, and also for a pair of a right-module and a left-module over any ring, with result an abelian group. Tensor products are important in areas of abstract algebra, homological algebra, algebraic topology, algebraic geometry, operator algebras and noncommutative geometry. The universal property of the tensor product of vector spaces extends to more general situations in abstract algebra. It allows the study of bilinear or multilinear operations via linear operations. The tensor product of an algebra and a module can be used for extension of scalars. For a commutative ring, the tensor product of modules can be iterated to form the tensor algebra of a module, allowing one to define multiplication in the module in a universal way.

In mathematics, a Lie bialgebra is the Lie-theoretic case of a bialgebra: it's a set with a Lie algebra and a Lie coalgebra structure which are compatible.

In algebraic geometry, a morphism of schemes generalizes a morphism of algebraic varieties just as a scheme generalizes an algebraic variety. It is, by definition, a morphism in the category of schemes.

In mathematics, especially in the field of representation theory, Schur functors are certain functors from the category of modules over a fixed commutative ring to itself. They generalize the constructions of exterior powers and symmetric powers of a vector space. Schur functors are indexed by Young diagrams in such a way that the horizontal diagram with n cells corresponds to the nth exterior power functor, and the vertical diagram with n cells corresponds to the nth symmetric power functor. If a vector space V is a representation of a group G, then $also has a natural action of G for any Schur functor .$

In mathematics, a symmetric tensor is a tensor that is invariant under a permutation of its vector arguments:

This is a glossary of algebraic geometry.

In mathematics, the tensor product of representations is a tensor product of vector spaces underlying representations together with the factor-wise group action on the product. This construction, together with the Clebsch–Gordan procedure, can be used to generate additional irreducible representations if one already knows a few.

This is a glossary of representation theory in mathematics.

References

Eisenbud, David; Harris, Joe, 3264 and All That: A Second Course in Algebraic Geometry

David Eisenbud is an American mathematician. He is a professor of mathematics at the University of California, Berkeley and was Director of the Mathematical Sciences Research Institute (MSRI) from 1997 to 2007. He was reappointed to this office in 2013, and his term has been extended until July 31, 2022.

Joseph Daniel Harris, known nearly universally as Joe Harris, is a mathematician at Harvard University working in the field of algebraic geometry. He attended college at and received his Ph.D. from Harvard in 1978 under Phillip Griffiths.

External links

Hopkins, Michael J. "Symmetric powers of the sphere" (PDF).

Michael Jerome Hopkins is an American mathematician known for work in algebraic topology.

This mathematics-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.