Table of vertex-symmetric digraphs

Last updated

The best known vertex transitive digraphs (as of October 2008) in the directed Degree diameter problem are tabulated below.

Contents

Table of the orders of the largest known vertex-symmetric graphs for the directed degree diameter problem

k
d
234567891011
26 [g 1] 10 [g 2] 20 [g 3] 27 [g 3] 72 [g 4] 144 [g 4] 171 [g 2] 336 [g 5] 504 [g 5] 737 [g 2]
312 [g 1] 27 [g 3] 60 [g 6] 165 [g 7] 333 [g 2] 1 152 [g 8] 2 041 [g 9] 5 115 [g 9] 11 568 [g 9] 41 472 [g 8]
420 [g 1] 60 [g 5] 168 [g 4] 465 [g 9] 1 378 [g 9] 7 200 [g 8] 14 400 [g 10] 42 309 [g 9] 137 370 [g 9] 648 000 [g 8]
530 [g 1] 120 [g 5] 360 [g 5] 1 152 [g 8] 3 775 [g 9] 28 800 [g 8] 86 400 [g 10] 259 200 [g 8] 1 010 658 [g 9] 5 184 000 [g 8]
642 [g 1] 210 [g 5] 840 [g 5] 2 520 [g 5] 9 020 [g 9] 88 200 [g 8] 352 800 [g 10] 1 411 200 [g 8] 5 184 000 [g 8] 27 783 000 [g 8]
756 [g 1] 336 [g 5] 1 680 [g 5] 6 720 [g 5] 20 160 [g 5] 225 792 [g 8] 1 128 960 [g 10] 5 644 800 [g 8] 27 783 000 [g 8] 113 799 168 [g 8]
872 [g 1] 504 [g 5] 3 024 [g 5] 15 120 [g 5] 60 480 [g 5] 508 032 [g 8] 3 048 192 [g 10] 18 289 152 [g 8] 113 799 168 [g 8] 457 228 800 [g 8]
990 [g 1] 720 [g 5] 5 040 [g 5] 30 240 [g 5] 151 200 [g 5] 1 036 800 [g 8] 7 257 600 [g 10] 50 803 200 [g 8] 384 072 192 [g 8] 1 828 915 200 [g 8]
10110 [g 1] 990 [g 5] 7 920 [g 5] 55 400 [g 5] 332 640 [g 5] 1 960 200 [g 8] 15 681 600 [g 10] 125 452 800 [g 8] 1 119 744 000 [g 8] 6 138 320 000 [g 8]
11132 [g 1] 1 320 [g 5] 11 880 [g 5] 95 040 [g 5] 665 280 [g 5] 3 991 680 [g 5] 31 152 000 [g 10] 282 268 800 [g 8] 2 910 897 000 [g 8] 18 065 203 200 [g 8]
12156 [g 1] 1 716 [g 5] 17 160 [g 5] 154 440 [g 5] 1 235 520 [g 5] 8 648 640 [g 5] 58 893 120 [g 10] 588 931 200 [g 8] 6 899 904 000 [g 8] 47 703 427 200 [g 8]
13182 [g 1] 2 184 [g 5] 24 024 [g 5] 240 240 [g 5] 2 162 160 [g 5] 17 297 280 [g 5] 121 080 960 [g 5] 1 154 305 152 [g 8] 15 159 089 098 [g 8] 115 430 515 200 [g 8]

The footnotes in the table indicate the origin of the digraph that achieves the given number of vertices:

  1. 1 2 3 4 5 6 7 8 9 10 11 12 Family of digraphs found by Kautz (1969).
  2. 1 2 3 4 Cayley digraphs found by Michael J. Dinneen. Details about these graphs are available in a paper by the author.
  3. 1 2 3 Cayley digraphs found by Michael J. Dinneen. The complete set of Cayley digraphs in that order was found by Eyal Loz.
  4. 1 2 3 Cayley digraphs found by Paul Hafner. Details about these graphs are available in a paper by the author.
  5. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 Family of digraphs found by Faber & Moore (1988).
  6. ↑ Digraph found by Faber & Moore (1988). The complete set of Cayley digraphs in that order was found by Eyal Loz.
  7. ↑ Cayley digraph found by Paul Hafner. The complete set of Cayley digraphs in that order was found by Eyal Loz.
  8. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 Digraphs found by Comellas & Fiol (1995).
  9. 1 2 3 4 5 6 7 8 9 10 Cayley digraphs found by Eyal Loz. More details are available in Loz & Širáň (2008).
  10. 1 2 3 4 5 6 7 8 9 Digraphs found by J. Gómez.

Related Research Articles

<span class="mw-page-title-main">Petersen graph</span> Cubic graph with 10 vertices and 15 edges

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

<span class="mw-page-title-main">Hamiltonian path</span> Path in a graph that visits each vertex exactly once

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. The computational problems of determining whether such paths and cycles exist in graphs are NP-complete; see Hamiltonian path problem for details.

<span class="mw-page-title-main">Cayley graph</span> Graph defined from a mathematical group

In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem, and uses a specified set of generators for the group. It is a central tool in combinatorial and geometric group theory. The structure and symmetry of Cayley graphs makes them particularly good candidates for constructing expander graphs.

<span class="mw-page-title-main">Pancake sorting</span> Mathematics problem

Pancake sorting is the mathematical problem of sorting a disordered stack of pancakes in order of size when a spatula can be inserted at any point in the stack and used to flip all pancakes above it. A pancake number is the minimum number of flips required for a given number of pancakes. In this form, the problem was first discussed by American geometer Jacob E. Goodman. A variant of the problem is concerned with burnt pancakes, where each pancake has a burnt side and all pancakes must, in addition, end up with the burnt side on bottom.

In the mathematical field of graph theory, an automorphism is a permutation of the vertices such that edges are mapped to edges and non-edges are mapped to non-edges. A graph is a vertex-transitive graph if, given any two vertices v1 and v2 of G, there is an automorphism f such that

<span class="mw-page-title-main">Connectivity (graph theory)</span> Basic concept of graph theory

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

<span class="mw-page-title-main">Algebraic graph theory</span> Branch of mathematics

Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches. There are three main branches of algebraic graph theory, involving the use of linear algebra, the use of group theory, and the study of graph invariants.

<span class="mw-page-title-main">Diameter (graph theory)</span> Longest distance between two vertices

In graph theory, the diameter of a connected undirected graph is the farthest distance between any two of its vertices. That is, it is the diameter of a set for the set of vertices of the graph, and for the shortest-path distance in the graph. Diameter may be considered either for weighted or for unweighted graphs. Researchers have studied the problem of computing the diameter, both in arbitrary graphs and in special classes of graphs.

<span class="mw-page-title-main">Brendan McKay (mathematician)</span> Australian mathematician

Brendan Damien McKay is an Australian computer scientist and mathematician. He is currently an Emeritus Professor in the Research School of Computer Science at the Australian National University (ANU). He has published extensively in combinatorics.

<span class="mw-page-title-main">Hoffman–Singleton graph</span> 7-regular undirected graph with 50 nodes and 175 edges

In the mathematical field of graph theory, the Hoffman–Singleton graph is a 7-regular undirected graph with 50 vertices and 175 edges. It is the unique strongly regular graph with parameters (50,7,0,1). It was constructed by Alan Hoffman and Robert Singleton while trying to classify all Moore graphs, and is the highest-order Moore graph known to exist. Since it is a Moore graph where each vertex has degree 7, and the girth is 5, it is a (7,5)-cage.

In graph theory, a Moore graph is a regular graph whose girth is more than twice its diameter. If the degree of such a graph is d and its diameter is k, its girth must equal 2k + 1. This is true, for a graph of degree d and diameter k, if and only if its number of vertices equals

In graph theory, the Lovász conjecture (1969) is a classical problem on Hamiltonian paths in graphs. It says:

<span class="mw-page-title-main">Directed graph</span> Graph with oriented edges

In mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by directed edges, often called arcs.

In graph theory, the degree diameter problem is the problem of finding the largest possible graph for a given maximum degree and diameter. The Moore bound sets limits on this, but for many years mathematicians in the field have been interested in a more precise answer. The table below gives current progress on this problem.

In graph theory, the degree diameter problem is the problem of finding the largest possible graph G of diameter k such that the largest degree of any of the vertices in G is at most d. The size of G is bounded above by the Moore bound; for 1 < k and 2 < d, only the Petersen graph, the Hoffman-Singleton graph, and possibly graphs of diameter k = 2 and degree d = 57 attain the Moore bound. In general, the largest degree-diameter graphs are much smaller in size than the Moore bound.

<span class="mw-page-title-main">Italo Jose Dejter</span>

Italo Jose Dejter is an Argentine-born American mathematician, a retired professor of mathematics and computer science from the University of Puerto Rico, and a researcher in algebraic topology, differential topology, graph theory, coding theory and combinatorial designs. He obtained a Licentiate degree in mathematics from University of Buenos Aires in 1967, arrived at Rutgers University in 1970 by means of a Guggenheim Fellowship and obtained a Ph.D. degree in mathematics in 1975 under the supervision of Professor Ted Petrie, with support of the National Science Foundation. He was a professor at the Federal University of Santa Catarina, Brazil, from 1977 to 1984, with grants from the National Council for Scientific and Technological Development, (CNPq).

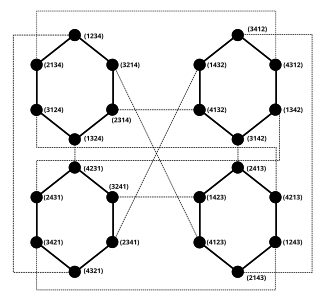
<span class="mw-page-title-main">Pancake graph</span>

In the mathematical field of graph theory, the pancake graphPn or n-pancake graph is a graph whose vertices are the permutations of n symbols from 1 to n and its edges are given between permutations transitive by prefix reversals.

<span class="mw-page-title-main">Second neighborhood problem</span> Unsolved problem about oriented graphs

In mathematics, the second neighborhood problem is an unsolved problem about oriented graphs posed by Paul Seymour. Intuitively, it suggests that in a social network described by such a graph, someone will have at least as many friends-of-friends as friends.

Mirka Miller was a Czech-Australian mathematician and computer scientist interested in graph theory and data security. She was a professor of electrical engineering and computer science at the University of Newcastle.

In graph theory, the McKay–Miller–Širáň graphs are an infinite class of vertex-transitive graphs with diameter two, and with a large number of vertices relative to their diameter and degree. They are named after Brendan McKay, Mirka Miller, and Jozef Širáň, who first constructed them using voltage graphs in 1998.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.