In mathematics, the theta operator is a differential operator defined by [1] [2]
This is sometimes also called the homogeneity operator, because its eigenfunctions are the monomials in z:
In n variables the homogeneity operator is given by
As in one variable, the eigenspaces of θ are the spaces of homogeneous functions. (Euler's homogeneous function theorem)
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.
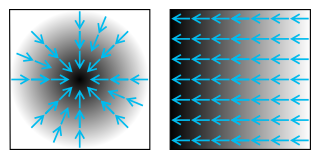
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field whose value at a point is the "direction and rate of fastest increase". If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to maximize a function by gradient ascent. In coordinate-free terms, the gradient of a function may be defined by:
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
In vector calculus, the Jacobian matrix of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and the determinant are often referred to simply as the Jacobian in literature.
In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation that accepts a function and returns another function.
In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.
In mathematics, the symmetry of second derivatives refers to the possibility of interchanging the order of taking partial derivatives of a function
In mathematics, integral equations are equations in which an unknown function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form:
In mathematics, the Schwarzian derivative is an operator similar to the derivative which is invariant under Möbius transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and hypergeometric functions. It plays an important role in the theory of univalent functions, conformal mapping and Teichmüller spaces. It is named after the German mathematician Hermann Schwarz.
In mathematics, a homogeneous function is a function of several variables such that, if all its arguments are multiplied by a scalar, then its value is multiplied by some power of this scalar, called the degree of homogeneity, or simply the degree; that is, if k is an integer, a function f of n variables is homogeneous of degree k if
In mathematics, an infinitesimal transformation is a limiting form of small transformation. For example one may talk about an infinitesimal rotation of a rigid body, in three-dimensional space. This is conventionally represented by a 3×3 skew-symmetric matrix A. It is not the matrix of an actual rotation in space; but for small real values of a parameter ε the transformation
In mathematics, the eigenvalue problem for the Laplace operator is known as the Helmholtz equation. It corresponds to the linear partial differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.
In mathematics, a homogeneous polynomial, sometimes called quantic in older texts, is a polynomial whose nonzero terms all have the same degree. For example, is a homogeneous polynomial of degree 5, in two variables; the sum of the exponents in each term is always 5. The polynomial is not homogeneous, because the sum of exponents does not match from term to term. The function defined by a homogeneous polynomial is always a homogeneous function.
In mathematics, the biharmonic equation is a fourth-order partial differential equation which arises in areas of continuum mechanics, including linear elasticity theory and the solution of Stokes flows. Specifically, it is used in the modeling of thin structures that react elastically to external forces.
In mathematical physics, a Grassmann number, named after Hermann Grassmann, is an element of the exterior algebra over the complex numbers. The special case of a 1-dimensional algebra is known as a dual number. Grassmann numbers saw an early use in physics to express a path integral representation for fermionic fields, although they are now widely used as a foundation for superspace, on which supersymmetry is constructed.
In differential calculus, there is no single uniform notation for differentiation. Instead, various notations for the derivative of a function or variable have been proposed by various mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation are listed below.
