
Brownian motion, or pedesis, is the random motion of particles suspended in a medium.

In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example, a particle trapped inside a large box can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow, quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never "sit still". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.

In quantum mechanics, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, x, and momentum, p, can be predicted from initial conditions.

In mathematics, the Dirac delta function, also known as the unit impulse symbol, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. It can also be interpreted as a linear functional that maps every function to its value at zero, or as the weak limit of a sequence of bump functions, which are zero over most of the real line, with a tall spike at the origin. Bump functions are thus sometimes called "approximate" or "nascent" delta functions.
Thermal conduction is the transfer of internal energy by microscopic collisions of particles and movement of electrons within a body. The colliding particles, which include molecules, atoms and electrons, transfer disorganized microscopic kinetic and potential energy, when joined known as internal energy. Conduction takes place in most phases: solid, liquid, and plasma.
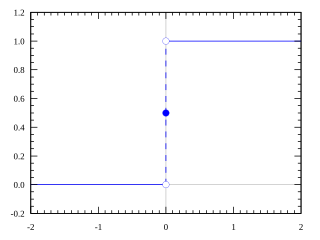
The Heaviside step function, or the unit step function, usually denoted by H or θ, is a step function, named after Oliver Heaviside (1850–1925), the value of which is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.

In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well.

The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.

In general relativity, Schwarzschild geodesics describe the motion of test particles in the gravitational field of a central fixed mass that is, motion in the Schwarzschild metric. Schwarzschild geodesics have been pivotal in the validation of Einstein's theory of general relativity. For example, they provide accurate predictions of the anomalous precession of the planets in the Solar System and of the deflection of light by gravity.
The diffusion of plasma across a magnetic field was conjectured to follow the Bohm diffusion scaling as indicated from the early plasma experiments of very lossy machines. This predicted that the rate of diffusion was linear with temperature and inversely linear with the strength of the confining magnetic field.
Catalyst poisoning refers to the partial or total deactivation of a catalyst by a chemical compound. Poisoning refers specifically to chemical deactivation, rather than other mechanisms of catalyst degradation such as thermal decomposition or physical damage. Although usually undesirable, poisoning may be helpful when it results in improved catalyst selectivity. An important historic example was the poisoning of catalytic converters by leaded fuel.
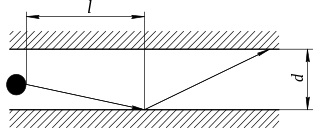
In physics, Knudsen diffusion, named after Martin Knudsen, is a means of diffusion that occurs when the scale length of a system is comparable to or smaller than the mean free path of the particles involved. An example of this is in a long pore with a narrow diameter (2–50 nm) because molecules frequently collide with the pore wall.

Spinodal decomposition occurs when one thermodynamic phase spontaneously separates into two phases. Decomposition occurs in the absence of nucleation because certain fluctuations in the system reduce the free energy. As a result, the phase change occurs immediately. There is no waiting, as there typically is when there is a nucleation barrier.

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition.
Murray's law predicts the thickness of branches in transport networks, such that the cost for transport and maintenance of the transport medium is minimized. This law is observed in the vascular and respiratory systems of animals, xylem in plants, and the respiratory system of insects. Its simplest version states that if a branch of radius splits into two branches of radii and , then . Like the Hagen–Poiseuille equation and Fick's laws, which were also formulated from a biological context, Murray's law is a basic physical principle for transfer networks.
Nuclear magnetic resonance (NMR) in porous materials covers the application of using NMR as a tool to study the structure of porous media and various processes occurring in them. This technique allows the determination of characteristics such as the porosity and pore size distribution, the permeability, the water saturation, the wettability, etc.
In mathematics, the Łukaszyk–Karmowski metric is a function defining a distance between two random variables or two random vectors. This function is not a metric as it does not satisfy the identity of indiscernibles condition of the metric, that is for two identical arguments its value is greater than zero. The concept is named after Szymon Łukaszyk and Wojciech Karmowski.

The hyperbolastic functions, also known as hyperbolastic growth models, are mathematical functions that are used in medical statistical modeling. These models were originally developed to capture the growth dynamics of multicellular tumor spheres, and were introduced in 2005 by Mohammad Tabatabai, David Williams, and Zoran Bursac. The precision of hyperbolastic functions in modeling real world problems is somewhat due to their flexibility in their point of inflection. These functions can be used in a wide variety of modeling problems such as tumor growth, stem cell proliferation, pharma kinetics, cancer growth, sigmoid activation function in neural networks, and epidemiological disease progression or regression.
The redundancy principle in biology expresses the need of many copies of the same entity to fulfill a biological function. Examples are numerous: disproportionate numbers of spermatozoa during fertilization compared to one egg, large number of neurotransmitters released during neuronal communication compared to the number of receptors, large numbers of released calcium ions during transient in cells and many more in molecular and cellular transduction or gene activation and cell signaling. This redundancy is particularly relevant when the sites of activation is physically separated from the initial position of the molecular messengers. The redundancy is often generated for the purpose of resolving the time constraint of fast-activating pathways. It can be expressed in terms of the theory of extreme statistics to determine its laws and quantify how shortest paths are selected. The main goal is to estimate these large numbers from physical principles and mathematical derivations.


























