
In geometry, the Thomson cubic of a triangle is the locus of centers of circumconics whose normals at the vertices are concurrent.

In geometry, the Thomson cubic of a triangle is the locus of centers of circumconics whose normals at the vertices are concurrent.

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
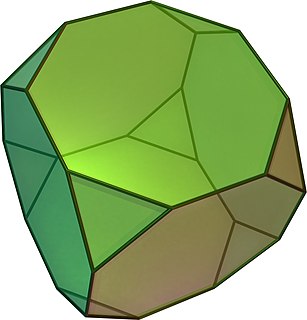
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.

In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation

In projective geometry, Pascal's theorem states that if six arbitrary points are chosen on a conic and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon meet at three points which lie on a straight line, called the Pascal line of the hexagon. It is named after Blaise Pascal.

In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.

In geometry, the isogonal conjugate of a point P with respect to a triangle ABC is constructed by reflecting the lines PA, PB, and PC about the angle bisectors of A, B, and C respectively. These three reflected lines concur at the isogonal conjugate of P. This is a direct result of the trigonometric form of Ceva's theorem.
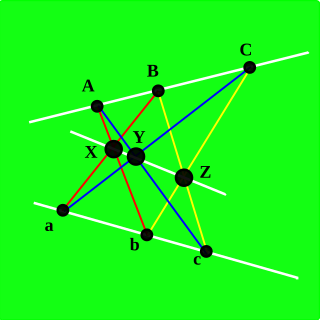
In geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point.

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.

The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton Conway calls it an oblate tetrahedrille or shortened to obtetrahedrille.
In triangle geometry, a triangle conic is a conic in the plane of the reference triangle and associated with it in some way. For example, the circumcircle and the incircle of the reference triangle are triangle conics. Other examples are the Steiner ellipse which is an ellipse passing through the vertices and having its centre at the centroid of the reference triangle, the Kiepert hyperbola which is a conic passing through the vertices, the centroid and the orthocentre of the reference triangle and the Artzt parabolas which are parabolas touching two sidelines of the reference triangle at vertices of the triangle. The terminology of triangle conic is widely used in the literature without a formal definition,that is, without precisely formulating the relations a conic should have with the reference triangle so as to qualify it to be called a triangle conic (see,). WolframMathWorld has a page titled "Triangle conics" which gives a list of 42 items without giving a definition of triangle conic. However, Paris Pamfilos in his extensive collection of topics in geometry and topics in other fields related to geometry defines a triangle conic as a "conic circumscribing a triangle ABC or inscribed in a triangle ". The terminology triangle circle is used to denote a circle associated with the reference triangle is some way.
The Catalogue of Triangle Cubics is an online resource containing detailed information about more than 1200 cubic curves in the plane of a reference triangle. The resource is maintained by Bernard Gilbert. Each cubic in the resource is assigned a unique identification number of the form "Knnn" where "nnn" denotes three digits. The identification number of the first entry in the catalogue is "K001" which is the Neuberg cubic of the reference triangle ABC. The catalogue provides, among other things, the following information about each of the cubics listed:
In Euclidean geometry, the Neuberg cubic is a special cubic plane curve associated with a reference triangle with several remarkable properties. It is named after Joseph Jean Baptiste Neuberg, a Luxembourger mathematician, who first introduced the curve in a paper published in 1884. The curve appears as the first item, with identification number K001, in Bernard Gilbert's Catalogue of Triangle Cubics which is a compilation of extensive information about more than 1200 triangle cubics.
In triangle geometry, a circumcevian triangle is a special triangle associated with the reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle.
In mathematics, in triangle geometry, McCay cubic is a cubic plane curve in the plane of the reference triangle and associated with it, and having several remarkable properties. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003.

In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.