The quantum Hall effect is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values

A polaron is a quasiparticle used in condensed matter physics to understand the interactions between electrons and atoms in a solid material. The polaron concept was proposed by Lev Landau in 1933 and Solomon Pekar in 1946 to describe an electron moving in a dielectric crystal where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. For comparison of the models proposed in these papers see M. I. Dykman and E. I. Rashba, The roots of polaron theory, Physics Today 68, 10 (2015). This lowers the electron mobility and increases the electron's effective mass.
In solid-state physics, the electron mobility characterises how quickly an electron can move through a metal or semiconductor when pulled by an electric field. There is an analogous quantity for holes, called hole mobility. The term carrier mobility refers in general to both electron and hole mobility.
The classical XY model is a lattice model of statistical mechanics. In general, the XY model can be seen as a specialization of Stanley's n-vector model for n = 2.
Jellium, also known as the uniform electron gas (UEG) or homogeneous electron gas (HEG), is a quantum mechanical model of interacting electrons in a solid where the positive charges are assumed to be uniformly distributed in space; the electron density is a uniform quantity as well in space. This model allows one to focus on the effects in solids that occur due to the quantum nature of electrons and their mutual repulsive interactions without explicit introduction of the atomic lattice and structure making up a real material. Jellium is often used in solid-state physics as a simple model of delocalized electrons in a metal, where it can qualitatively reproduce features of real metals such as screening, plasmons, Wigner crystallization and Friedel oscillations.
The Berezinskii–Kosterlitz–Thouless transition is a phase transition of the two-dimensional (2-D) XY model in statistical physics. It is a transition from bound vortex-antivortex pairs at low temperatures to unpaired vortices and anti-vortices at some critical temperature. The transition is named for condensed matter physicists Vadim Berezinskii, John M. Kosterlitz and David J. Thouless. BKT transitions can be found in several 2-D systems in condensed matter physics that are approximated by the XY model, including Josephson junction arrays and thin disordered superconducting granular films. More recently, the term has been applied by the 2-D superconductor insulator transition community to the pinning of Cooper pairs in the insulating regime, due to similarities with the original vortex BKT transition.
In condensed matter physics, Anderson localization is the absence of diffusion of waves in a disordered medium. This phenomenon is named after the American physicist P. W. Anderson, who was the first to suggest that electron localization is possible in a lattice potential, provided that the degree of randomness (disorder) in the lattice is sufficiently large, as can be realized for example in a semiconductor with impurities or defects.
Fluorescence correlation spectroscopy (FCS) is a statistical analysis, via time correlation, of stationary fluctuations of the fluorescence intensity. Its theoretical underpinning originated from L. Onsager's regression hypothesis. The analysis provides kinetic parameters of the physical processes underlying the fluctuations. One of the interesting applications of this is an analysis of the concentration fluctuations of fluorescent particles (molecules) in solution. In this application, the fluorescence emitted from a very tiny space in solution containing a small number of fluorescent particles (molecules) is observed. The fluorescence intensity is fluctuating due to Brownian motion of the particles. In other words, the number of the particles in the sub-space defined by the optical system is randomly changing around the average number. The analysis gives the average number of fluorescent particles and average diffusion time, when the particle is passing through the space. Eventually, both the concentration and size of the particle (molecule) are determined. Both parameters are important in biochemical research, biophysics, and chemistry.

In condensed matter physics, Hofstadter's butterfly is a graph of the spectral properties of non-interacting two-dimensional electrons in a perpendicular magnetic field in a lattice. The fractal, self-similar nature of the spectrum was discovered in the 1976 Ph.D. work of Douglas Hofstadter and is one of the early examples of modern scientific data visualization. The name reflects the fact that, as Hofstadter wrote, "the large gaps [in the graph] form a very striking pattern somewhat resembling a butterfly."
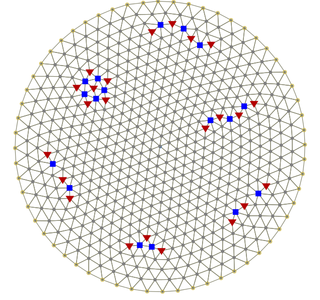
A Wigner crystal is the solid (crystalline) phase of electrons first predicted by Eugene Wigner in 1934. A gas of electrons moving in a uniform, inert, neutralizing background will crystallize and form a lattice if the electron density is less than a critical value. This is because the potential energy dominates the kinetic energy at low densities, so the detailed spatial arrangement of the electrons becomes important. To minimize the potential energy, the electrons form a bcc lattice in 3D, a triangular lattice in 2D and an evenly spaced lattice in 1D. Most experimentally observed Wigner clusters exist due to the presence of the external confinement, i.e. external potential trap. As a consequence, deviations from the b.c.c or triangular lattice are observed. A crystalline state of the 2D electron gas can also be realized by applying a sufficiently strong magnetic field. However, it is still not clear whether it is the Wigner crystallization that has led to observation of insulating behaviour in magnetotransport measurements on 2D electron systems, since other candidates are present, such as Anderson localization.
In quantum field theory and statistical mechanics, the Mermin–Wagner theorem states that continuous symmetries cannot be spontaneously broken at finite temperature in systems with sufficiently short-range interactions in dimensions d ≤ 2. Intuitively, this means that long-range fluctuations can be created with little energy cost and since they increase the entropy they are favored.
The Bose–Hubbard model gives a description of the physics of interacting spinless bosons on a lattice. It is closely related to the Hubbard model which originated in solid-state physics as an approximate description of superconducting systems and the motion of electrons between the atoms of a crystalline solid. The model was first introduced by Gersch and Knollman in 1963 in the context of granular superconductors. The model rose to prominence in the 1980s after it was found to capture the essence of the superfluid-insulator transition in a way that was much more mathematically tractable than fermionic metal-insulator models.
Quantum dissipation is the branch of physics that studies the quantum analogues of the process of irreversible loss of energy observed at the classical level. Its main purpose is to derive the laws of classical dissipation from the framework of quantum mechanics. It shares many features with the subjects of quantum decoherence and quantum theory of measurement.
In condensed matter physics, biexcitons are created from two free excitons.
The SP formula for the dephasing rate of a particle that moves in a fluctuating environment unifies various results that have been obtained, notably in condensed matter physics, with regard to the motion of electrons in a metal. The general case requires to take into account not only the temporal correlations but also the spatial correlations of the environmental fluctuations. These can be characterized by the spectral form factor , while the motion of the particle is characterized by its power spectrum . Consequently, at finite temperature the expression for the dephasing rate takes the following form that involves S and P functions:
The kicked rotator, also spelled as kicked rotor, is a paradigmatic model for both Hamiltonian chaos and quantum chaos. It describes a free rotating stick in an inhomogeneous "gravitation like" field that is periodically switched on in short pulses. The model is described by the Hamiltonian
Thomas C. Spencer is an American mathematical physicist, known in particular for important contributions to constructive quantum field theory, statistical mechanics, and spectral theory of random operators. He earned his doctorate in 1972 from New York University with a dissertation entitled Perturbation of the Po2 Quantum Field Hamiltonian written under the direction of James Glimm. Since 1986, he has been professor of mathematics at the Institute for Advanced Study. He is a member of the United States National Academy of Sciences, and the recipient of the Dannie Heineman Prize for Mathematical Physics.
Many-body localization (MBL) is a dynamical phenomenon occurring in isolated many-body quantum systems. It is characterized by the system failing to reach thermal equilibrium, and retaining a memory of its initial condition in local observables for infinite times.
The KTHNY-theory describes melting of crystals in two dimensions (2D). The name is derived from the initials of the surnames of John Michael Kosterlitz, David J. Thouless, Bertrand Halperin, David R. Nelson, and A. Peter Young, who developed the theory in the 1970s. It is, beside the Ising model in 2D and the XY model in 2D, one of the few theories, which can be solved analytically and which predicts a phase transition at a temperature .
The quantum boomerang effect is a quantum mechanical phenomenon whereby wavepackets launched through disordered media return, on average, to their starting points, as a consequence of Anderson localization and the inherent symmetries of the system. At early times, the initial parity asymmetry of the nonzero momentum leads to asymmetric behavior: nonzero displacement of the wavepackets from their origin. At long times, inherent time-reversal symmetry and the confining effects of Anderson localization lead to correspondingly symmetric behavior: both zero final velocity and zero final displacement.





