Related Research Articles

In mathematics, differential topology is the field dealing with the topological properties and smooth properties of smooth manifolds. In this sense differential topology is distinct from the closely related field of differential geometry, which concerns the geometric properties of smooth manifolds, including notions of size, distance, and rigid shape. By comparison differential topology is concerned with coarser properties, such as the number of holes in a manifold, its homotopy type, or the structure of its diffeomorphism group. Because many of these coarser properties may be captured algebraically, differential topology has strong links to algebraic topology.
In the mathematical field of geometric topology, the Poincaré conjecture is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.
In mathematics, Thurston's geometrization conjecture states that each of certain three-dimensional topological spaces has a unique geometric structure that can be associated with it. It is an analogue of the uniformization theorem for two-dimensional surfaces, which states that every simply connected Riemann surface can be given one of three geometries . In three dimensions, it is not always possible to assign a single geometry to a whole topological space. Instead, the geometrization conjecture states that every closed 3-manifold can be decomposed in a canonical way into pieces that each have one of eight types of geometric structure. The conjecture was proposed by William Thurston (1982), and implies several other conjectures, such as the Poincaré conjecture and Thurston's elliptization conjecture.

Grigori Yakovlevich Perelman is a Russian mathematician who is known for his contributions to the fields of geometric analysis, Riemannian geometry, and geometric topology. In 2005, Perelman abruptly quit his research job at the Steklov Institute of Mathematics, and in 2006 stated that he had quit professional mathematics, due to feeling disappointed over the ethical standards in the field. He lives in seclusion in Saint Petersburg, and has not accepted offers for interviews since 2006.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional linear subspace σp of the tangent space at a point p of the manifold. It can be defined geometrically as the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a real-valued function on the 2-Grassmannian bundle over the manifold.
In the mathematical field of Riemannian geometry, the scalar curvature is a measure of the curvature of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the geometry of the metric near that point. It is defined by a complicated explicit formula in terms of partial derivatives of the metric components, although it is also characterized by the volume of infinitesimally small geodesic balls. In the context of the differential geometry of surfaces, the scalar curvature is twice the Gaussian curvature, and completely characterizes the curvature of a surface. In higher dimensions, however, the scalar curvature only represents one particular part of the Riemann curvature tensor.
In mathematics, the uniformization theorem says that every simply connected Riemann surface is conformally equivalent to one of three Riemann surfaces: the open unit disk, the complex plane, or the Riemann sphere. The theorem is a generalization of the Riemann mapping theorem from simply connected open subsets of the plane to arbitrary simply connected Riemann surfaces.
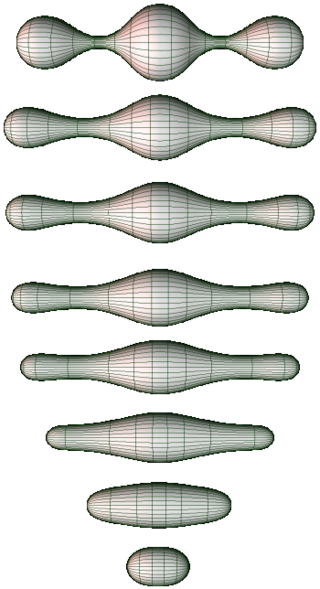
In the mathematical fields of differential geometry and geometric analysis, the Ricci flow, sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation.

Shing-Tung Yau is a Chinese-American mathematician and the William Caspar Graustein Professor of Mathematics at Harvard University. In April 2022, Yau announced retirement from Harvard to become Chair Professor of mathematics at Tsinghua University.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.

Richard Streit Hamilton is an American mathematician who serves as the Davies Professor of Mathematics at Columbia University. He is known for contributions to geometric analysis and partial differential equations. Hamilton is best known for foundational contributions to the theory of the Ricci flow and the development of a corresponding program of techniques and ideas for resolving the Poincaré conjecture and geometrization conjecture in the field of geometric topology. Grigori Perelman built upon Hamilton's results to prove the conjectures, and was awarded a Millennium Prize for his work. However, Perelman declined the award, regarding Hamilton's contribution as being equal to his own.

Mikhael Leonidovich Gromov is a Russian-French mathematician known for his work in geometry, analysis and group theory. He is a permanent member of Institut des Hautes Études Scientifiques in France and a professor of mathematics at New York University.

In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In mathematics, more precisely in topology and differential geometry, a hyperbolic 3-manifold is a manifold of dimension 3 equipped with a hyperbolic metric, that is a Riemannian metric which has all its sectional curvatures equal to −1. It is generally required that this metric be also complete: in this case the manifold can be realised as a quotient of the 3-dimensional hyperbolic space by a discrete group of isometries.
In mathematics, Hopf conjecture may refer to one of several conjectural statements from differential geometry and topology attributed to Heinz Hopf.

In the mathematical field of knot theory, the hyperbolic volume of a hyperbolic link is the volume of the link's complement with respect to its complete hyperbolic metric. The volume is necessarily a finite real number, and is a topological invariant of the link. As a link invariant, it was first studied by William Thurston in connection with his geometrization conjecture.
The Geometry Festival is an annual mathematics conference held in the United States.

John William Lott is a professor of Mathematics at the University of California, Berkeley. He is known for contributions to differential geometry.
References
For the proof of the conjectures, see the references in the articles on geometrization conjecture or Poincaré conjecture.
- William Thurston. Three-dimensional geometry and topology. Vol. 1. Edited by Silvio Levy. Princeton Mathematical Series, 35. Princeton University Press, Princeton, NJ, 1997. x+311 pp. ISBN 0-691-08304-5.
- William Thurston. The Geometry and Topology of Three-Manifolds, 1980 Princeton lecture notes on geometric structures on 3-manifolds, that states his elliptization conjecture near the beginning of section 3.