 | This article may be confusing or unclear to readers.(December 2013) |
The Tienstra formula is used to solve the resection problem in surveying, by which the location of a given point is determined by observations of angles to known landmarks from the unknown point.
J. M. Tienstra (1895-1951) was a professor of the Delft university of Technology where he taught the use of barycentric coordinates in solving the resection problem. It seems most probable that his name became attached to the procedure for this reason, though when, and by whom, the formula was first proposed is unknown. [1]
The resection problem consists in finding the location of an observer by measuring the angles subtended by lines of sight from the observer to three known points. Tienstra’s formula provides the most compact and elegant solution to this problem. [2]
Where:
In geometry and algebra, a real number is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots.
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .
In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.
In complex analysis, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. The residue theorem should not be confused with special cases of the generalized Stokes' theorem; however, the latter can be used as an ingredient of its proof.
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.
In algebra, a cubic equation in one variable is an equation of the form
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up more than a century later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation.
Atmospheric refraction is the deviation of light or other electromagnetic wave from a straight line as it passes through the atmosphere due to the variation in air density as a function of height. This refraction is due to the velocity of light through air decreasing with increased density. Atmospheric refraction near the ground produces mirages. Such refraction can also raise or lower, or stretch or shorten, the images of distant objects without involving mirages. Turbulent air can make distant objects appear to twinkle or shimmer. The term also applies to the refraction of sound. Atmospheric refraction is considered in measuring the position of both celestial and terrestrial objects.
Position resection and intersection are methods for determining an unknown geographic position by measuring angles with respect to known positions. In resection, the one point with unknown coordinates is occupied and sightings are taken to the known points; in intersection, the two points with known coordinates are occupied and sightings are taken to the unknown point.
Trigonometry is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios such as sine.
Solution of triangles is the main trigonometric problem of finding the characteristics of a triangle, when some of these are known. The triangle can be located on a plane or on a sphere. Applications requiring triangle solutions include geodesy, astronomy, construction, and navigation.
In trigonometry, the Snellius–Pothenot problem is a problem first described in the context of planar surveying. Given three known points A, B, C, an observer at an unknown point P observes that the line segment AC subtends an angle α and the segment CB subtends an angle β; the problem is to determine the position of the point P..
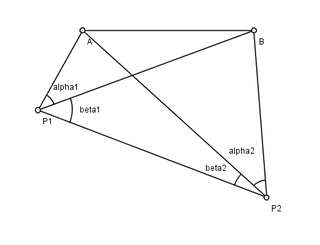
In trigonometry, Hansen's problem is a problem in planar surveying, named after the astronomer Peter Andreas Hansen (1795–1874), who worked on the geodetic survey of Denmark. There are two known points A, B, and two unknown points P1, P2. From P1 and P2 an observer measures the angles made by the lines of sight to each of the other three points. The problem is to find the positions of P1 and P2. See figure; the angles measured are (α1, β1, α2, β2).
The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an oblate ellipsoid, a slightly flattened sphere. A geodesic is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry.
In geometry, the Weber problem, named after Alfred Weber, is one of the most famous problems in location theory. It requires finding a point in the plane that minimizes the sum of the transportation costs from this point to n destination points, where different destination points are associated with different costs per unit distance.
The quadratrix or trisectrix of Hippias is a curve which is created by a uniform motion. It is one of the oldest examples for a kinematic curve. Its discovery is attributed to the Greek sophist Hippias of Elis, who used it around 420 BC in an attempt to solve the angle trisection problem. Later around 350 BC Dinostratus used it in an attempt to solve the problem of squaring the circle.
 | This engineering-related article is a stub. You can help Wikipedia by expanding it. |
