
In mathematics, differential topology is the field dealing with the topological properties and smooth properties of smooth manifolds. In this sense differential topology is distinct from the closely related field of differential geometry, which concerns the geometric properties of smooth manifolds, including notions of size, distance, and rigid shape. By comparison differential topology is concerned with coarser properties, such as the number of holes in a manifold, its homotopy type, or the structure of its diffeomorphism group. Because many of these coarser properties may be captured algebraically, differential topology has strong links to algebraic topology.

In mathematics, a diffeomorphism is an isomorphism of smooth manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are differentiable.
In the mathematical field of geometric topology, the Poincaré conjecture is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.

In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.

In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional linear subspace σp of the tangent space at a point p of the manifold. It can be defined geometrically as the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a real-valued function on the 2-Grassmannian bundle over the manifold.
In mathematical physics, a closed timelike curve (CTC) is a world line in a Lorentzian manifold, of a material particle in spacetime, that is "closed", returning to its starting point. This possibility was first discovered by Willem Jacob van Stockum in 1937 and later confirmed by Kurt Gödel in 1949, who discovered a solution to the equations of general relativity (GR) allowing CTCs known as the Gödel metric; and since then other GR solutions containing CTCs have been found, such as the Tipler cylinder and traversable wormholes. If CTCs exist, their existence would seem to imply at least the theoretical possibility of time travel backwards in time, raising the spectre of the grandfather paradox, although the Novikov self-consistency principle seems to show that such paradoxes could be avoided. Some physicists speculate that the CTCs which appear in certain GR solutions might be ruled out by a future theory of quantum gravity which would replace GR, an idea which Stephen Hawking labeled the chronology protection conjecture. Others note that if every closed timelike curve in a given space-time passes through an event horizon, a property which can be called chronological censorship, then that space-time with event horizons excised would still be causally well behaved and an observer might not be able to detect the causal violation.
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the requirement of positive-definiteness is relaxed.
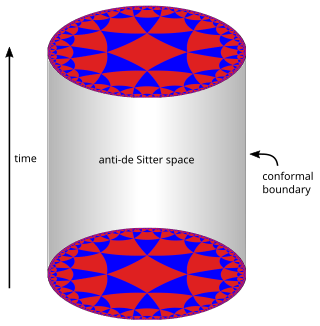
In mathematics and physics, n-dimensional anti-de Sitter space (AdSn) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In the mathematical field of differential geometry, Ricci-flatness is a condition on the curvature of a (pseudo-)Riemannian manifold. Ricci-flat manifolds are a special kind of Einstein manifold. In theoretical physics, Ricci-flat Lorentzian manifolds are of fundamental interest, as they are the solutions of Einstein's field equations in vacuum with vanishing cosmological constant.
In the mathematical field of differential geometry, there are various splitting theorems on when a pseudo-Riemannian manifold can be given as a metric product. The best-known is the Cheeger–Gromoll splitting theorem for Riemannian manifolds, although there has also been research into splitting of Lorentzian manifolds.
In mathematics, real projective space, denoted or is the topological space of lines passing through the origin 0 in the real space It is a compact, smooth manifold of dimension n, and is a special case of a Grassmannian space.

In mathematics, a symmetric space is a Riemannian manifold whose group of symmetries contains an inversion symmetry about every point. This can be studied with the tools of Riemannian geometry, leading to consequences in the theory of holonomy; or algebraically through Lie theory, which allowed Cartan to give a complete classification. Symmetric spaces commonly occur in differential geometry, representation theory and harmonic analysis.
In the mathematical field of Lorentzian geometry, a Cauchy surface is a certain kind of submanifold of a Lorentzian manifold. In the application of Lorentzian geometry to the physics of general relativity, a Cauchy surface is usually interpreted as defining an "instant of time"; in the mathematics of general relativity, Cauchy surfaces are important in the formulation of the Einstein equations as an evolutionary problem.
On a Lorentzian manifold, certain curves are distinguished as timelike. A timelike homotopy between two timelike curves is a homotopy such that each intermediate curve is timelike. No closed timelike curve (CTC) on a Lorentzian manifold is timelike homotopic to a point ; such a manifold is therefore said to be multiply connected by timelike curves. A manifold such as the 3-sphere can be simply connected, and at the same time be timelike multiply connected. Equivalence classes of timelike homotopic curves define their own fundamental group, as noted by Smith (1967). A smooth topological feature which prevents a CTC from being deformed to a point may be called a timelike topological feature.
In mathematical physics, global hyperbolicity is a certain condition on the causal structure of a spacetime manifold. It is called hyperbolic in analogy with the linear theory of wave propagation, where the future state of a system is specified by initial conditions. This is relevant to Albert Einstein's theory of general relativity, and potentially to other metric gravitational theories.
In mathematics, the Cartan–Hadamard theorem is a statement in Riemannian geometry concerning the structure of complete Riemannian manifolds of non-positive sectional curvature. The theorem states that the universal cover of such a manifold is diffeomorphic to a Euclidean space via the exponential map at any point. It was first proved by Hans Carl Friedrich von Mangoldt for surfaces in 1881, and independently by Jacques Hadamard in 1898. Élie Cartan generalized the theorem to Riemannian manifolds in 1928. The theorem was further generalized to a wide class of metric spaces by Mikhail Gromov in 1987; detailed proofs were published by Ballmann (1990) for metric spaces of non-positive curvature and by Alexander & Bishop (1990) for general locally convex metric spaces.
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.






