 | This article relies largely or entirely on a single source .(May 2024) |
Top-hat filters are several real-space or Fourier space filtering techniques. [1] The name top-hat originates from the shape of the filter, which is a rectangle function, when viewed in the domain in which the filter is constructed.
In real-space the filter performs nearest-neighbour filtering, incorporating components from neighbouring y-function values. Despite its ease of implementation, its practical use is limited as the real-space representation of a top-hat filter is the sinc function, which has the often undesirable effect of incorporating non-local frequencies.
Exact non-digital implementations are only theoretically possible. Top-hat filters can be constructed by chaining theoretical low-band and high-band filters. In practice, an approximate top-hat filter can be constructed in analogue hardware using approximate low-band and high-band filters.
In Fourier space, a top hat filter selects a band of signal of desired frequency by the specification of lower and upper bounding frequencies. Top-hat filters are particularly easy to implement digitally.
The top hat function can be generated by differentiating a linear ramp function of width . The limit of then becomes the Dirac delta function. Its real-space form is the same as the moving average, with the exception of not introducing a shift in the output function.
Linear filters process time-varying input signals to produce output signals, subject to the constraint of linearity. In most cases these linear filters are also time invariant in which case they can be analyzed exactly using LTI system theory revealing their transfer functions in the frequency domain and their impulse responses in the time domain. Real-time implementations of such linear signal processing filters in the time domain are inevitably causal, an additional constraint on their transfer functions. An analog electronic circuit consisting only of linear components will necessarily fall in this category, as will comparable mechanical systems or digital signal processing systems containing only linear elements. Since linear time-invariant filters can be completely characterized by their response to sinusoids of different frequencies, they are sometimes known as frequency filters.
The Nyquist–Shannon sampling theorem is an essential principle for digital signal processing linking the frequency range of a signal and the sample rate required to avoid a type of distortion called aliasing. The theorem states that the sample rate must be at least twice the bandwidth of the signal to avoid aliasing. In practice, it is used to select band-limiting filters to keep aliasing below an acceptable amount when an analog signal is sampled or when sample rates are changed within a digital signal processing function.
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.
A low-pass filter is a filter that passes signals with a frequency lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency. The exact frequency response of the filter depends on the filter design. The filter is sometimes called a high-cut filter, or treble-cut filter in audio applications. A low-pass filter is the complement of a high-pass filter.
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function.
Filter design is the process of designing a signal processing filter that satisfies a set of requirements, some of which may be conflicting. The purpose is to find a realization of the filter that meets each of the requirements to an acceptable degree.
In signal processing, sampling is the reduction of a continuous-time signal to a discrete-time signal. A common example is the conversion of a sound wave to a sequence of "samples". A sample is a value of the signal at a point in time and/or space; this definition differs from the term's usage in statistics, which refers to a set of such values.
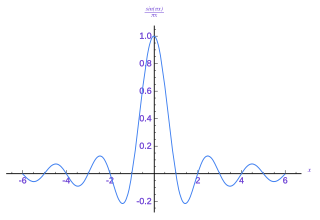
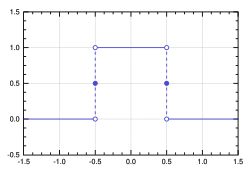
In signal processing, a sinc filter can refer to either a sinc-in-time filter whose impulse response is a sinc function and whose frequency response is rectangular, or to a sinc-in-frequency filter whose impulse response is rectangular and whose frequency response is a sinc function. Calling them according to which domain the filter resembles a sinc avoids confusion. If the domain is unspecified, sinc-in-time is often assumed, or context hopefully can infer the correct domain.
A spectrum analyzer measures the magnitude of an input signal versus frequency within the full frequency range of the instrument. The primary use is to measure the power of the spectrum of known and unknown signals. The input signal that most common spectrum analyzers measure is electrical; however, spectral compositions of other signals, such as acoustic pressure waves and optical light waves, can be considered through the use of an appropriate transducer. Spectrum analyzers for other types of signals also exist, such as optical spectrum analyzers which use direct optical techniques such as a monochromator to make measurements.
Bandlimiting refers to a process which reduces the energy of a signal to an acceptably low level outside of a desired frequency range.
Delta-sigma modulation is an oversampling method for encoding signals into low bit depth digital signals at a very high sample-frequency as part of the process of delta-sigma analog-to-digital converters (ADCs) and digital-to-analog converters (DACs). Delta-sigma modulation achieves high quality by utilizing a negative feedback loop during quantization to the lower bit depth that continuously corrects quantization errors and moves quantization noise to higher frequencies well above the original signal's bandwidth. Subsequent low-pass filtering for demodulation easily removes this high frequency noise and time averages to achieve high accuracy in amplitude which can be ultimately encoded as pulse-code modulation (PCM).
In the areas of computer vision, image analysis and signal processing, the notion of scale-space representation is used for processing measurement data at multiple scales, and specifically enhance or suppress image features over different ranges of scale. A special type of scale-space representation is provided by the Gaussian scale space, where the image data in N dimensions is subjected to smoothing by Gaussian convolution. Most of the theory for Gaussian scale space deals with continuous images, whereas one when implementing this theory will have to face the fact that most measurement data are discrete. Hence, the theoretical problem arises concerning how to discretize the continuous theory while either preserving or well approximating the desirable theoretical properties that lead to the choice of the Gaussian kernel. This article describes basic approaches for this that have been developed in the literature.
In electronics and signal processing, mainly in digital signal processing, a Gaussian filter is a filter whose impulse response is a Gaussian function. Gaussian filters have the properties of having no overshoot to a step function input while minimizing the rise and fall time. This behavior is closely connected to the fact that the Gaussian filter has the minimum possible group delay. A Gaussian filter will have the best combination of suppression of high frequencies while also minimizing spatial spread, being the critical point of the uncertainty principle. These properties are important in areas such as oscilloscopes and digital telecommunication systems.
In electronics and telecommunications, pulse shaping is the process of changing a transmitted pulses' waveform to optimize the signal for its intended purpose or the communication channel. This is often done by limiting the bandwidth of the transmission and filtering the pulses to control intersymbol interference. Pulse shaping is particularly important in RF communication for fitting the signal within a certain frequency band and is typically applied after line coding and modulation.
In mathematics, Wiener deconvolution is an application of the Wiener filter to the noise problems inherent in deconvolution. It works in the frequency domain, attempting to minimize the impact of deconvolved noise at frequencies which have a poor signal-to-noise ratio.
The method of reassignment is a technique for sharpening a time-frequency representation by mapping the data to time-frequency coordinates that are nearer to the true region of support of the analyzed signal. The method has been independently introduced by several parties under various names, including method of reassignment, remapping, time-frequency reassignment, and modified moving-window method. The method of reassignment sharpens blurry time-frequency data by relocating the data according to local estimates of instantaneous frequency and group delay. This mapping to reassigned time-frequency coordinates is very precise for signals that are separable in time and frequency with respect to the analysis window.
In statistical signal processing, the goal of spectral density estimation (SDE) or simply spectral estimation is to estimate the spectral density of a signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities.
In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from percussion instruments; most noticeable are the pre-echos. The term "ringing" is because the output signal oscillates at a fading rate around a sharp transition in the input, similar to a bell after being struck. As with other artifacts, their minimization is a criterion in filter design.
In signal processing, a filter is a device or process that removes some unwanted components or features from a signal. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal. Most often, this means removing some frequencies or frequency bands. However, filters do not exclusively act in the frequency domain; especially in the field of image processing many other targets for filtering exist. Correlations can be removed for certain frequency components and not for others without having to act in the frequency domain. Filters are widely used in electronics and telecommunication, in radio, television, audio recording, radar, control systems, music synthesis, image processing, computer graphics, and structural dynamics.
Overcompleteness is a concept from linear algebra that is widely used in mathematics, computer science, engineering, and statistics. It was introduced by R. J. Duffin and A. C. Schaeffer in 1952.
