
In mathematics, a plane real algebraic curve is the set of points on the Euclidean plane whose coordinates are zeros of some polynomial in two variables. More generally an algebraic curve is similar but may be embedded in a higher dimensional space or defined over some more general field.
In mathematics, two functions have a contact of order k if, at a point P, they have the same value and k equal derivatives. This is an equivalence relation, whose equivalence classes are generally called jets. The point of osculation is also called the double cusp. Contact is a geometric notion; it can be defined algebraically as a valuation.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
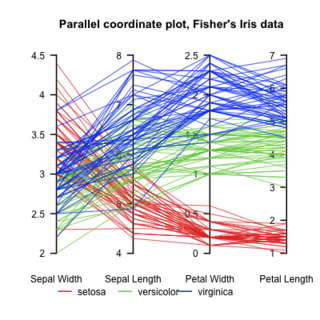
Parallel coordinates are a common way of visualizing high-dimensional geometry and analyzing multivariate data.
In mathematics, a branched surface is a generalization of both surfaces and train tracks.
In mathematics, a branched manifold is a generalization of a differentiable manifold which may have singularities of very restricted type and admits a well-defined tangent space at each point. A branched n-manifold is covered by n-dimensional "coordinate charts", each of which involves one or several "branches" homeomorphically projecting into the same differentiable n-disk in Rn. Branched manifolds first appeared in the dynamical systems theory, in connection with one-dimensional hyperbolic attractors constructed by Smale and were formalized by R. F. Williams in a series of papers on expanding attractors. Special cases of low dimensions are known as train tracks and branched surfaces and play prominent role in the geometry of three-manifolds after Thurston.

In knot theory, a branch of mathematics, a knot or link in the 3-dimensional sphere is called fibered or fibred if there is a 1-parameter family of Seifert surfaces for , where the parameter runs through the points of the unit circle , such that if is not equal to then the intersection of and is exactly .

Three-dimensional space is a geometric setting in which three values are required to determine the position of an element. This is the informal meaning of the term dimension.
In mathematics, an elliptic surface is a surface that has an elliptic fibration, in other words a proper morphism with connected fibers to an algebraic curve such that almost all fibers are smooth curves of genus 1. This is equivalent to the generic fiber being a smooth curve of genus one. This follows from proper base change.
In mathematics, a Zariski geometry consists of an abstract structure introduced by Ehud Hrushovski and Boris Zilber, in order to give a characterisation of the Zariski topology on an algebraic curve, and all its powers. The Zariski topology on a product of algebraic varieties is very rarely the product topology, but richer in closed sets defined by equations that mix two sets of variables. The result described gives that a very definite meaning, applying to projective curves and compact Riemann surfaces in particular.
In mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.
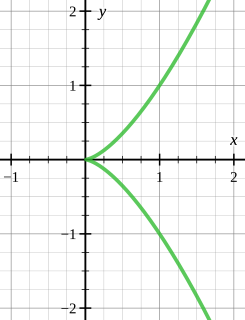
In mathematics a cusp, sometimes called spinode in old texts, is a point on a curve where a moving point on the curve must start to move backward. A typical example is given in the figure. A cusp is thus a type of singular point of a curve.

In the geometry of planar curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature, and some authors define a vertex to be more specifically a local extreme point of curvature. However, other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant. For space curves, on the other hand, a vertex is a point where the torsion vanishes.
In mathematical physics, global hyperbolicity is a certain condition on the causal structure of a spacetime manifold. This is relevant to Einstein's theory of general relativity, and potentially to other metric gravitational theories.
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution without any fixed points. Skew-symmetric graphs are identical to the double covering graphs of bidirected graphs.

In topology, a branch of mathematics, a lamination is a :
A railway or railroad is a track where the vehicle travels over two parallel steel bars, called rails. The rails support and guide the wheels of the vehicles, which are traditionally either trains or trams. Modern light rail is a relatively new innovation which combines aspects of those two modes of transport. However fundamental differences in the track and wheel design are important, especially where trams or light railways and trains have to share a section of track, as sometimes happens in congested areas.

In geometry, a convex curve is a simple curve in the Euclidean plane which lies completely on one side of each and every one of its tangent lines.
In astronomy, geography, and related sciences and contexts, a direction or plane passing by a given point is said to be vertical if it contains the local gravity direction at that point. Conversely, a direction or plane is said to be horizontal if it is perpendicular to the vertical direction.


















