
Rayleigh scattering, named after the nineteenth-century British physicist Lord Rayleigh, is the predominantly elastic scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of the radiation. For light frequencies well below the resonance frequency of the scattering particle, the amount of scattering is inversely proportional to the fourth power of the wavelength.

Numerical climate models use quantitative methods to simulate the interactions of the important drivers of climate, including atmosphere, oceans, land surface and ice. They are used for a variety of purposes from study of the dynamics of the climate system to projections of future climate. Climate models may also be qualitative models and also narratives, largely descriptive, of possible futures.
The Eddington luminosity, also referred to as the Eddington limit, is the maximum luminosity a body can achieve when there is balance between the force of radiation acting outward and the gravitational force acting inward. The state of balance is called hydrostatic equilibrium. When a star exceeds the Eddington luminosity, it will initiate a very intense radiation-driven stellar wind from its outer layers. Since most massive stars have luminosities far below the Eddington luminosity, their winds are mostly driven by the less intense line absorption. The Eddington limit is invoked to explain the observed luminosity of accreting black holes such as quasars.

Neutron transport is the study of the motions and interactions of neutrons with materials. Nuclear scientists and engineers often need to know where neutrons are in an apparatus, what direction they are going, and how quickly they are moving. It is commonly used to determine the behavior of nuclear reactor cores and experimental or industrial neutron beams. Neutron transport is a type of radiative transport.
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission, and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in a wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media, with complex multiple scattering effects, numerical methods are required. The present article is largely focused on the condition of radiative equilibrium.
A runaway greenhouse effect occurs when a planet's atmosphere contains greenhouse gas in an amount sufficient to block thermal radiation from leaving the planet, preventing the planet from cooling and from having liquid water on its surface. A runaway version of the greenhouse effect can be defined by a limit on a planet's outgoing longwave radiation which is asymptotically reached due to higher surface temperatures evaporating a condensable species into the atmosphere, increasing its optical depth. This positive feedback means the planet cannot cool down through longwave radiation and continues to heat up until it can radiate outside of the absorption bands of the condensable species.
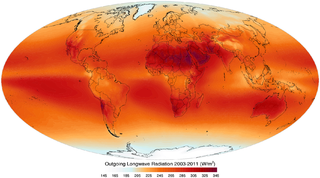
Outgoing Long-wave Radiation (OLR) is electromagnetic radiation of wavelengths from 3–100 μm emitted from Earth and its atmosphere out to space in the form of thermal radiation. It is also referred to as up-welling long-wave radiation and terrestrial long-wave flux, among others. The flux of energy transported by outgoing long-wave radiation is measured in W/m2. In the Earth's climate system, long-wave radiation involves processes of absorption, scattering, and emissions from atmospheric gases, aerosols, clouds and the surface.

Discrete dipole approximation (DDA), also known as coupled dipole approximation, is a method for computing scattering of radiation by particles of arbitrary shape and by periodic structures. Given a target of arbitrary geometry, one seeks to calculate its scattering and absorption properties by an approximation of the continuum target by a finite array of small polarizable dipoles. This technique is used in a variety of applications including nanophotonics, radar scattering, aerosol physics and astrophysics.
An atmospheric radiative transfer model, code, or simulator calculates radiative transfer of electromagnetic radiation through a planetary atmosphere.
Light scattering by particles is the process by which small particles scatter light causing optical phenomena such as the blue color of the sky, and halos.
Streamer is a radiative transfer code to calculate radiances (intensities) or irradiances in the atmosphere.
DISORT - general and versatile plane-parallel radiative transfer program applicable to problems from the ultraviolet to the radar regions of the electromagnetic spectrum.
The air mass coefficient defines the direct optical path length through the Earth's atmosphere, expressed as a ratio relative to the path length vertically upwards, i.e. at the zenith. The air mass coefficient can be used to help characterize the solar spectrum after solar radiation has traveled through the atmosphere.
Radiative equilibrium is the condition where the total thermal radiation leaving an object is equal to the total thermal radiation entering it. It is one of the several requirements for thermodynamic equilibrium, but it can occur in the absence of thermodynamic equilibrium. There are various types of radiative equilibrium, which is itself a kind of dynamic equilibrium.
Codes for electromagnetic scattering by spheres - this article list codes for electromagnetic scattering by a homogeneous sphere, layered sphere, and cluster of spheres.
The Grey atmosphere is a useful set of approximations made for radiative transfer applications in studies of stellar atmospheres based on the simplification that the absorption coefficient of matter within the atmosphere is constant for all frequencies of incident radiation.
With increased interest in sea ice and its effects on the global climate, efficient methods are required to monitor both its extent and exchange processes. Satellite-mounted, microwave radiometers, such SSMI, AMSR and AMSU, are an ideal tool for the task because they can see through cloud cover, and they have frequent, global coverage. A passive microwave instrument detects objects through emitted radiation since different substance have different emission spectra. To detect sea ice more efficiently, there is a need to model these emission processes. The interaction of sea ice with electromagnetic radiation in the microwave range is still not well understood. In general is collected information limited because of the large-scale variability due to the emissivity of sea ice.
DART is a 3D radiative transfer model, designed for scientific research, in particular remote sensing. Developed at CESBIO since 1992, DART model was patented in 2003. It is freeware for scientific activities.
In the theory of radiative transfer, of either thermal or neutron radiation, a position and direction-dependent intensity function is usually sought for the description of the radiation field. The intensity field can in principle be solved from the integrodifferential radiative transfer equation (RTE), but an exact solution is usually impossible and even in the case of geometrically simple systems can contain unusual special functions such as the Chandrasekhar's H-function and Chandrasekhar's X- and Y-functions. The method of discrete ordinates, or the Sn method, is one way to approximately solve the RTE by discretizing both the xyz-domain and the angular variables that specify the direction of radiation. The methods were developed by Subrahmanyan Chandrasekhar when he was working on radiative transfer.
Schwarzschild's equation is used to calculate radiative transfer – energy transfer – through a medium in local thermodynamic equilibrium that both absorbs and emits electromagnetic radiation.