Two-tree broadcast

Last updated March 28, 2023

The two-tree broadcast (abbreviated 2tree-broadcast or 23-broadcast) is an algorithm that implements a broadcast communication pattern on a distributed system using message passing. A broadcast is a commonly used collective operation that sends data from one processor to all other processors. The two-tree broadcast communicates concurrently over two binary trees that span all processors. This achieves full usage of the bandwidth in the full-duplex communication model while having a startup latency logarithmic in the number of partaking processors.^[1] The algorithm can also be adapted to perform a reduction or prefix sum.

Algorithm

A broadcast sends a message from a specified root processor to all other processors. Binary tree broadcasting uses a binary tree to model the communication between the processors. Each processor corresponds to one node in the tree, and the root processor is the root of the tree. To broadcast a message $M$ , the root sends $M$ to its two children (child nodes). Each processor waits until it receives $M$ and then sends $M$ to its children. Because leaves have no children, they don't have to send any messages. The broadcasting process can be pipelined by splitting the message into $k$ blocks, which are then broadcast consecutively. In such a binary tree, the leaves of the tree only receive data, but never send any data themselves. If the communication is bidirectional (full-duplex), meaning each processor can send a message and receive a message at the same time, the leaves only use one half of the available bandwidth.

The idea of the two-tree broadcast is to use two binary trees $T 1$ and $T 2$ and communicate on both concurrently.^[1] The trees are constructed so that the interior nodes of one tree correspond to leaf nodes of the other tree. The data that has to be broadcast is split into blocks of equal size. In each step of the algorithm, each processor receives one block and sends the previous block to one of its children in the tree in which it is an interior node. A schedule is needed so that no processor has to send or receive two messages in the same step. To create such a schedule, the edges of both trees are colored with 0 and 1 such that

no processor is connected to its parent nodes in $T 1$ and $T 2$ using edges of the same color
no processor is connected to its children nodes in $T 1$ or $T 2$ using edges of the same color.

Edges with color 0 are used in even steps, edges with color 1 are used in odd steps. This schedule allows each processor to send one message and receive one message in each step, fully utilizing the available bandwidth.^[1]
Assume that processor $i$ wants to broadcast a message. The two trees are constructed for the remaining processors. Processor $i$ sends blocks alternating to the roots of the two trees, so each tree broadcasts one half of the message.

Analysis

Let $p$ be the number of processing elements (PE), numbered from $0$ to $p - 1$ .

Construction of the trees

Two-trees of size 6, 12, 7, 9 using mirroring (top) and shifting (bottom). T1 in red, T2 in blue. Two-trees.svg — Two-trees of size 6, 12, 7, 9 using mirroring (top) and shifting (bottom). $T 1$ in red, $T 2$ in blue.

Let $h = ⌈log(p + 2)⌉$ . $T 1$ and $T 2$ can be constructed as trees of height $h - 1$ , such that both trees form an in-order numbering of the processors, with the following method:^[1]
$T 1$ : If $p = 2 h - 2$ , $T 1$ is a complete binary tree of height $h - 1$ except that the rightmost leaf is missing. Otherwise, $T 1$ consists of a complete binary tree of height $h - 2$ covering PEs $[0, 2 h -1 - 2]$ , a recursively constructed tree covering PEs $[2 h -1, p - 1]$ , and a root at PE $2 h -1 - 1$ whose children are the roots of the left and the right subtree.
$T 2$ : There are two ways to construct $T 2$ . With shifting, $T 2$ is first constructed like $T 1$ , except that it contains an additional processor. Then $T 2$ is shifted by one position to the left and the leftmost leaf is removed. With mirroring, $T 2$ is the mirror image of $T 1$ (with the mirror axis between processors $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}p/2−1$ and $p / 2$ ). Mirroring only works for even $p$ .

It can be proven that a coloring with the desired properties exists for all $p$ .^[1] When mirroring is used to construct $T 2$ , each processor can independently compute the color of its incident edges in $O (log p)$ time.^[1]

Communication Time

For this analysis, the following communication model is used: A message of size $n$ has a communication time of $α + βn$ , independent on which processors communicate. $α$ represents the startup overhead to send the message, $β$ represents the transmission time per data element.^[2]

Suppose the message of size $m$ is split into $2 k$ blocks. Each communication step takes time $α + β m / 2 k$ . Let $h =log p$ be the height of the communication structure with the root at processor $i$ and the two trees below it. After $2 h$ steps, the first data block has reached every node in both trees. Afterwards, each processor receives one block in every step until it received all blocks. The total number of steps is $2 h + 2 k$ resulting in a total communication time of $(2 h + 2 k)(α + β m / 2 k)$ . Using an optimal $k = k* = (βmh/2α).mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1⁄2$ , the total communication time is $βm + 2 α log p + \sqrt 8 αβm log p$ .

Comparison to similar algorithms

In a linear pipeline broadcast, the message is split into $k$ blocks. In each step, each processor $i$ receives one block from the processor $i -1 (mod p)$ and sends one block to the processor $i +1 (mod p)$ . Linear pipeline has optimal throughput, but has a startup time in $O (p)$ .^[3] For large $p$ , the $O (log p)$ startup latency of the two-tree broadcast is faster. Because both algorithms have optimal throughput, the two-tree algorithm is faster for a large numbers of processors.

A binomial tree broadcast communicates along a binomial tree. Each process receives the message that is broadcast (the root already has the message) and then sends the message to its children. A binomial tree broadcast has only half the startup time of the two-tree broadcast, but a factor of $log(p)$ more communication.^[4] The binomial tree broadcast is faster than the two-tree broadcast for small messages, but slower for large messages.

A pipelined binary tree broadcast splits the message into $k$ blocks and broadcasts the blocks consecutively over a binary tree. By using a Fibonacci tree instead of a simple balanced binary tree, the startup latency can be reduced to $α log(p)$ . ^[5] A Fibonacci tree of height $h$ consists of a root that has a Fibonacci tree of height $h -1$ as its left child and a Fibonacci tree of $h -2$ as its right child. The pipelined Fibonacci tree broadcast has half the startup latency of the two-tree broadcast, but also only half of the throughput. It is faster for small messages, while the two-tree broadcast is faster for large messages.

Usage for other communication primitives

Reduction

A reduction (MPI_Reduce in the MPI standard) computes ${\textstyle \bigoplus _{i=0}^{p-1}M_{i}}$ where $M i$ is a vector of length $m$ originally available at processor $i$ and ${\textstyle \bigoplus }$ is a binary operation that is associative, but not necessarily commutative. The result is stored at a specified root processor $r$ .

Assume that $r = 0$ or $r = p -1$ . In this case the communication is identical to the broadcast, except that the communication direction is reversed.^[1] Each process receives two blocks from its children, reduces them with its own block, and sends the result to its parent. The root takes turns receiving blocks from the roots of $T 1$ and $T 2$ and reduces them with its own data. The communication time is the same as for the Broadcast and the amount of data reduced per processor is $2 m$ .
If the reduce operation is commutative, the result can be achieved for any root by renumbering the processors.

If the operation is not commutative and the root is not $0$ or $p -1$ , then $2 βm$ is a lower bound for the communication time.^[1] In this case, the remaining processors are split into two subgroups. The processors $< r$ perform a reduction to the root $r -1$ and the processors $> r$ perform a reduction to the root $r +1$ . Processor $r$ receives blocks alternating from the two roots of the subgroups.

Prefix sum

A prefix sum (MPI_Scan) computes ${\textstyle \bigoplus _{i=0}^{j}M_{i}}$ for each processor $j$ where $M i$ is a vector of length $m$ originally available at processor $i$ and ${\textstyle \bigoplus }$ is a binary associative operation. Using an inorder binary tree, a prefix sum can be computed by first performing an up-phase in which each interior node computes a partial sum ${\textstyle \bigoplus _{i=l}^{r}M_{i}}$ for left- and rightmost leaves $l$ and $r$ , followed by a down-phase in which prefixes of the form ${\textstyle \bigoplus _{i=0}^{l-1}M_{i}}$ are sent down the tree and allow each processor to finish computing its prefix sum.^[6]^[1] The communication in the up-phase is equivalent to a reduction to processor $0$ and the communication in the down-phase is equivalent to a broadcast from the processor $0$ . The total communication time is about twice the communication time of the two-tree broadcast.^[1]

ESBT broadcast

If $p$ is a power of two, there is an optimal broadcasting algorithm based on edge disjoint spanning binomial trees (ESBT) in a hypercube.^[7] The hypercube, excluding the root $0 d$ , is split into $log p$ ESBTs. The algorithm uses pipelining by splitting the broadcast data into $k$ blocks. Processor $0 d$ cyclically distributes blocks to the roots of the ESBTs and each ESBT performs a pipelined binary tree broadcast. In step $i$ , each processor sends and receives one message along dimension $i mod d$ . The communication time of the algorithm is $βm + α log p + \sqrt 4 αβm log p$ ,^[7] so the startup latency is only one half of the startup latency of the two-tree broadcast.
The drawback of the ESBT broadcast is that it does not work for other values of $p$ and it cannot be adapted for (non-commutative) reduction or prefix sum.

Related Research Articles

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code proceeds by means of Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".

<span class="mw-page-title-main">Heap (data structure)</span> Computer science data structure

In computer science, a heap is a specialized tree-based data structure which is essentially an almost complete tree that satisfies the heap property: in a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.

In computer science, a priority queue is an abstract data-type similar to a regular queue or stack data structure. Each element in a priority queue has an associated priority. In a priority queue, elements with high priority are served before elements with low priority. In some implementations, if two elements have the same priority, they are served in the same order that they were enqueued in. In other implementations, the order of elements with the same priority is undefined.

In the field of data compression, Shannon–Fano coding, named after Claude Shannon and Robert Fano, is a name given to two different but related techniques for constructing a prefix code based on a set of symbols and their probabilities.

<span class="mw-page-title-main">Binary heap</span> Variant of heap data structure

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.

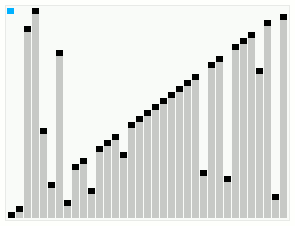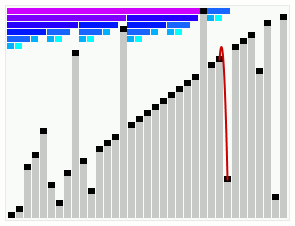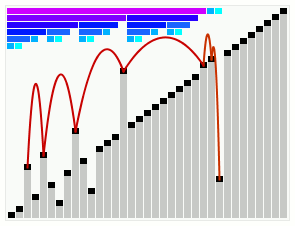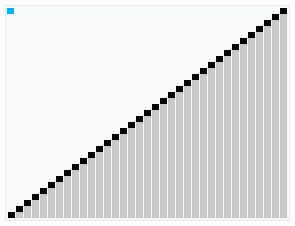
<span class="mw-page-title-main">Smoothsort</span> Comparison-based sorting algorithm

In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of $O (n log n)$ , but it is not a stable sort. The advantage of smoothsort is that it comes closer to $O (n)$ time if the input is already sorted to some degree, whereas heapsort averages $O (n log n)$ regardless of the initial sorted state.

In computer science, a Fibonacci heap is a data structure for priority queue operations, consisting of a collection of heap-ordered trees. It has a better amortized running time than many other priority queue data structures including the binary heap and binomial heap. Michael L. Fredman and Robert E. Tarjan developed Fibonacci heaps in 1984 and published them in a scientific journal in 1987. Fibonacci heaps are named after the Fibonacci numbers, which are used in their running time analysis.

In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.

In computer science, corecursion is a type of operation that is dual to recursion. Whereas recursion works analytically, starting on data further from a base case and breaking it down into smaller data and repeating until one reaches a base case, corecursion works synthetically, starting from a base case and building it up, iteratively producing data further removed from a base case. Put simply, corecursive algorithms use the data that they themselves produce, bit by bit, as they become available, and needed, to produce further bits of data. A similar but distinct concept is generative recursion which may lack a definite "direction" inherent in corecursion and recursion.

In graph theory, an m-ary tree is a rooted tree in which each node has no more than m children. A binary tree is the special case where m = 2, and a ternary tree is another case with m = 3 that limits its children to three.

A fundamental problem in distributed computing and multi-agent systems is to achieve overall system reliability in the presence of a number of faulty processes. This often requires coordinating processes to reach consensus, or agree on some data value that is needed during computation. Example applications of consensus include agreeing on what transactions to commit to a database in which order, state machine replication, and atomic broadcasts. Real-world applications often requiring consensus include cloud computing, clock synchronization, PageRank, opinion formation, smart power grids, state estimation, control of UAVs, load balancing, blockchain, and others.

In computer science, the prefix sum, cumulative sum, inclusive scan, or simply scan of a sequence of numbers $x 0, x 1, x 2, ...$ is a second sequence of numbers $y 0, y 1, y 2, ...$ , the sums of prefixes of the input sequence:

The distributed minimum spanning tree (MST) problem involves the construction of a minimum spanning tree by a distributed algorithm, in a network where nodes communicate by message passing. It is radically different from the classical sequential problem, although the most basic approach resembles Borůvka's algorithm. One important application of this problem is to find a tree that can be used for broadcasting. In particular, if the cost for a message to pass through an edge in a graph is significant, an MST can minimize the total cost for a source process to communicate with all the other processes in the network.

In distributed computing, leader election is the process of designating a single process as the organizer of some task distributed among several computers (nodes). Before the task has begun, all network nodes are either unaware which node will serve as the "leader" of the task, or unable to communicate with the current coordinator. After a leader election algorithm has been run, however, each node throughout the network recognizes a particular, unique node as the task leader.

<span class="mw-page-title-main">Fenwick tree</span>

A Fenwick tree or binary indexed tree(BIT) is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.

Collective operations are building blocks for interaction patterns, that are often used in SPMD algorithms in the parallel programming context. Hence, there is an interest in efficient realizations of these operations.

In computer science, the reduction operator is a type of operator that is commonly used in parallel programming to reduce the elements of an array into a single result. Reduction operators are associative and often commutative. The reduction of sets of elements is an integral part of programming models such as Map Reduce, where a reduction operator is applied (mapped) to all elements before they are reduced. Other parallel algorithms use reduction operators as primary operations to solve more complex problems. Many reduction operators can be used for broadcasting to distribute data to all processors.

$-dimensional hypercube is a network topology for parallel computers with processing elements. The topology allows for an efficient implementation of some basic communication primitives such as Broadcast, All-Reduce, and Prefix sum. The processing elements are numbered through . Each processing element is adjacent to processing elements whose numbers differ in one and only one bit. The algorithms described in this page utilize this structure efficiently.$

Broadcast is a collective communication primitive in parallel programming to distribute programming instructions or data to nodes in a cluster. It is the reverse operation of reduce. The broadcast operation is widely used in parallel algorithms, such as matrix-vector multiplication, Gaussian elimination and shortest paths.

References

1 2 3 4 5 6 7 8 9 10 Sanders, Peter; Speck, Jochen; Träff, Jesper Larsson (2009). "Two-tree algorithms for full bandwidth broadcast, reduction and scan". Parallel Computing. 35 (12): 581–594. doi:10.1016/j.parco.2009.09.001. ISSN 0167-8191.
↑ Hockney, Roger W. (1994). "The communication challenge for MPP: Intel Paragon and Meiko CS-2". Parallel Computing. 20 (3): 389–398. doi:10.1016/S0167-8191(06)80021-9. ISSN 0167-8191.
↑ Pješivac-Grbović, Jelena; Angskun, Thara; Bosilca, George; Fagg, Graham E.; Gabriel, Edgar; Dongarra, Jack J. (2007). "Performance analysis of MPI collective operations". Cluster Computing. 10 (2): 127–143. doi:10.1007/s10586-007-0012-0. ISSN 1386-7857. S2CID 2142998.
↑ Chan, Ernie; Heimlich, Marcel; Purkayastha, Avi; Van De Geijn, Rober (2007). "Collective Communication: Theory, Practice, and Experience". Concurrency and Computation: Practice and Experience. 19 (13): 1749–1783. doi:10.1002/cpe.v19:13. ISSN 1532-0626.
↑ Bruck, Jehoshua; Cypher, Robert; Ho, C-T (1992). Multiple message broadcasting with generalized Fibonacci trees (PDF). Parallel and Distributed Processing, 1992. Proceedings of the Fourth IEEE Symposium on. IEEE. pp. 424–431. doi:10.1109/SPDP.1992.242714. ISBN 978-0-8186-3200-6. S2CID 2846661.
↑ Sanders, Peter; Träff, Jesper Larsson (2006). Parallel Prefix (Scan) algorithms for MPI. European Parallel Virtual Machine/Message Passing Interface Users' Group Meeting. Lecture Notes in Computer Science. Vol. 4192. Springer. pp. 49–57. CiteSeerX 10.1.1.495.5815 . doi:10.1007/11846802_15. ISBN 978-3-540-39110-4. ISSN 0302-9743.
1 2 Johnsson, S.L.; Ho, C.-T. (1989). "Optimum broadcasting and personalized communication in hypercubes". IEEE Transactions on Computers. 38 (9): 1249–1268. doi:10.1109/12.29465. ISSN 0018-9340.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[SandersSpeck2009-1] 1 2 3 4 5 6 7 8 9 10 Sanders, Peter; Speck, Jochen; Träff, Jesper Larsson (2009). "Two-tree algorithms for full bandwidth broadcast, reduction and scan". Parallel Computing. 35 (12): 581–594. doi:10.1016/j.parco.2009.09.001. ISSN 0167-8191.

[Hockney1994-2] Hockney, Roger W. (1994). "The communication challenge for MPP: Intel Paragon and Meiko CS-2". Parallel Computing. 20 (3): 389–398. doi:10.1016/S0167-8191(06)80021-9. ISSN 0167-8191.

[Pješivac-GrbovićAngskun2007-3] Pješivac-Grbović, Jelena; Angskun, Thara; Bosilca, George; Fagg, Graham E.; Gabriel, Edgar; Dongarra, Jack J. (2007). "Performance analysis of MPI collective operations". Cluster Computing. 10 (2): 127–143. doi:10.1007/s10586-007-0012-0. ISSN 1386-7857. S2CID 2142998.

[ChanHeimlich2007-4] Chan, Ernie; Heimlich, Marcel; Purkayastha, Avi; Van De Geijn, Rober (2007). "Collective Communication: Theory, Practice, and Experience". Concurrency and Computation: Practice and Experience. 19 (13): 1749–1783. doi:10.1002/cpe.v19:13. ISSN 1532-0626.

[BruckCypher1992-5] Bruck, Jehoshua; Cypher, Robert; Ho, C-T (1992). Multiple message broadcasting with generalized Fibonacci trees (PDF). Parallel and Distributed Processing, 1992. Proceedings of the Fourth IEEE Symposium on. IEEE. pp. 424–431. doi:10.1109/SPDP.1992.242714. ISBN 978-0-8186-3200-6. S2CID 2846661.

[SandersTräff2006-6] Sanders, Peter; Träff, Jesper Larsson (2006). Parallel Prefix (Scan) algorithms for MPI. European Parallel Virtual Machine/Message Passing Interface Users' Group Meeting. Lecture Notes in Computer Science. Vol. 4192. Springer. pp. 49–57. CiteSeerX 10.1.1.495.5815 . doi:10.1007/11846802_15. ISBN 978-3-540-39110-4. ISSN 0302-9743.

[JohnssonHo1989-7] 1 2 Johnsson, S.L.; Ho, C.-T. (1989). "Optimum broadcasting and personalized communication in hypercubes". IEEE Transactions on Computers. 38 (9): 1249–1268. doi:10.1109/12.29465. ISSN 0018-9340.

[1]

[2]

[3]

[4]

[5]

[6]

[7]