
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as
In mathematics, de Moivre's formula states that for any real number x and integer n it holds that

Exponentiation is a mathematical operation, written as bn, involving two numbers, the baseb and the exponent or powern, and pronounced as "b raised to the power of n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.

In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two different parameterizations in common use:
- With a shape parameter k and a scale parameter θ.
- With a shape parameter α = k and an inverse scale parameter β = 1/θ, called a rate parameter.
In computer science, the Floyd–Warshall algorithm is an algorithm for finding shortest paths in a directed weighted graph with positive or negative edge weights. A single execution of the algorithm will find the lengths of shortest paths between all pairs of vertices. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm. Versions of the algorithm can also be used for finding the transitive closure of a relation , or widest paths between all pairs of vertices in a weighted graph.
In mathematics, an nth root of a number x is a number r which, when raised to the power n, yields x:

In mathematics, an identity is an equality relating one mathematical expression A to another mathematical expression B, such that A and B produce the same value for all values of the variables within a certain range of validity. In other words, A = B is an identity if A and B define the same functions, and an identity is an equality between functions that are differently defined. For example, and are identities. Identities are sometimes indicated by the triple bar symbol ≡ instead of =, the equals sign.
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. The terms "distribution" and "family" are often used loosely: specifically, an exponential family is a set of distributions, where the specific distribution varies with the parameter; however, a parametric family of distributions is often referred to as "a distribution", and the set of all exponential families is sometimes loosely referred to as "the" exponential family. They are distinct because they possess a variety of desirable properties, most importantly the existence of a sufficient statistic.

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
In mathematics, the Clausen function, introduced by Thomas Clausen (1832), is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other special functions. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.
In information geometry, the Fisher information metric is a particular Riemannian metric which can be defined on a smooth statistical manifold, i.e., a smooth manifold whose points are probability measures defined on a common probability space. It can be used to calculate the informational difference between measurements.
In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ of a distribution that models X. Formally, it is the variance of the score, or the expected value of the observed information. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior. The role of the Fisher information in the asymptotic theory of maximum-likelihood estimation was emphasized by the statistician Ronald Fisher. The Fisher information is also used in the calculation of the Jeffreys prior, which is used in Bayesian statistics.

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
In mathematics, the Mahler measureof a polynomial with complex coefficients is defined as

In number theory, the divisor summatory function is a function that is a sum over the divisor function. It frequently occurs in the study of the asymptotic behaviour of the Riemann zeta function. The various studies of the behaviour of the divisor function are sometimes called divisor problems.
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.
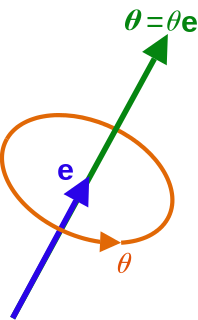
In mathematics, the axis–angle representation of a rotation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector e indicating the direction of an axis of rotation, and an angle θ describing the magnitude of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector e rooted at the origin because the magnitude of e is constrained. For example, the elevation and azimuth angles of e suffice to locate it in any particular Cartesian coordinate frame.
In image analysis, the generalized structure tensor (GST) is an extension of the Cartesian structure tensor to curvilinear coordinates. It is mainly used to detect and to represent the "direction" parameters of curves, just as the Cartesian structure tensor detects and represents the direction in Cartesian coordinates. Curve families generated by pairs of locally orthogonal functions have been the best studied.





















