Additive synthesis is a sound synthesis technique that creates timbre by adding sine waves together.
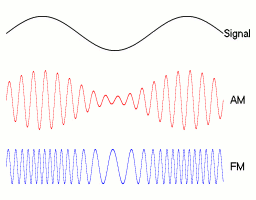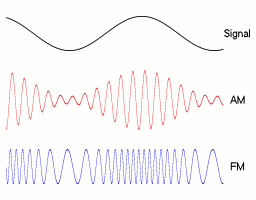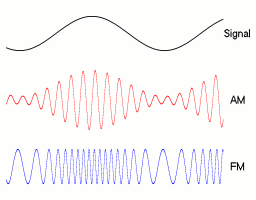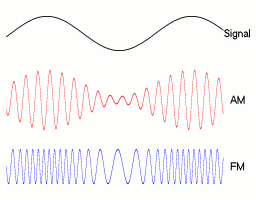
Frequency modulation (FM) is the encoding of information in a carrier wave by varying the instantaneous frequency of the wave. The technology is used in telecommunications, radio broadcasting, signal processing, and computing.

In physics and mathematics, the phase of a periodic function of some real variable is an angle-like quantity representing the number of periods spanned by that variable. It is denoted and expressed in such a scale that it varies by one full turn as the variable goes through each period. It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or as the variable completes a full period.
Phase modulation (PM) is a modulation pattern for conditioning communication signals for transmission. It encodes a message signal as variations in the instantaneous phase of a carrier wave. Phase modulation is one of the two principal forms of angle modulation, together with frequency modulation.
The amplitude of a periodic variable is a measure of its change in a single period. There are various definitions of amplitude, which are all functions of the magnitude of the differences between the variable's extreme values. In older texts, the phase of a period function is sometimes called the amplitude.

In electrical engineering, electrical impedance is the measure of the opposition that a circuit presents to a current when a voltage is applied.

In electronics, acoustics, and related fields, the waveform of a signal is the shape of its graph as a function of time, independent of its time and magnitude scales and of any displacement in time.

The sawtooth wave is a kind of non-sinusoidal waveform. It is so named based on its resemblance to the teeth of a plain-toothed saw with a zero rake angle. A single sawtooth, or an intermittently triggered sawtooth, is called a ramp waveform.
A chirp is a signal in which the frequency increases (up-chirp) or decreases (down-chirp) with time. In some sources, the term chirp is used interchangeably with sweep signal. It is commonly applied to sonar, radar, and laser systems, and to other applications, such as in spread-spectrum communications. This signal type is biologically inspired and occurs as a phenomenon due to dispersion. It is usually compensated for by using a matched filter, which can be part of the propagation channel. Depending on the specific performance measure, however, there are better techniques both for radar and communication. Since it was used in radar and space, it has been adopted also for communication standards. For automotive radar applications, it is usually called linear frequency modulated waveform (LFMW).

The power spectrum of a time series describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal as analyzed in terms of its frequency content, is called its spectrum.

A spectrogram is a visual representation of the spectrum of frequencies of a signal as it varies with time. When applied to an audio signal, spectrograms are sometimes called sonographs, voiceprints, or voicegrams. When the data are represented in a 3D plot they may be called waterfalls.

In electronics, ring modulation is a signal processing function, an implementation of frequency mixing, performed by creating multiple frequencies from those of the two signals, where one is typically a sine wave or another simple waveform and the other is the signal to be modulated. A ring modulator is an electronic device for ring modulation. A ring modulator may be used in music synthesizers and as an effects unit.

A square wave is a non-sinusoidal periodic waveform in which the amplitude alternates at a steady frequency between fixed minimum and maximum values, with the same duration at minimum and maximum. In an ideal square wave, the transitions between minimum and maximum are instantaneous.

A sine wave or sinusoid is a mathematical curve that describes a smooth periodic oscillation. A sine wave is a continuous wave. It is named after the function sine, of which it is the graph. It occurs often in both pure and applied mathematics, as well as physics, engineering, signal processing and many other fields. Its most basic form as a function of time (t) is:

Intermodulation (IM) or intermodulation distortion (IMD) is the amplitude modulation of signals containing two or more different frequencies, caused by nonlinearities or time variance in a system. The intermodulation between frequency components will form additional components at frequencies that are not just at harmonic frequencies of either, like harmonic distortion, but also at the sum and difference frequencies of the original frequencies and at sums and differences of multiples of those frequencies.
In mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components. The real and imaginary parts of an analytic signal are real-valued functions related to each other by the Hilbert transform.
In statistical signal processing, the goal of spectral density estimation (SDE) is to estimate the spectral density of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities.
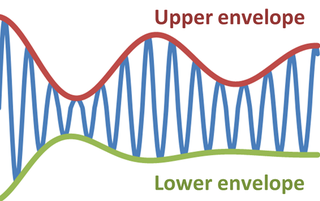
In physics and engineering, the envelope of an oscillating signal is a smooth curve outlining its extremes. The envelope thus generalizes the concept of a constant amplitude into an instantaneous amplitude. The figure illustrates a modulated sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, space, angle, or indeed of any variable.
In rotordynamics, order tracking is a family of signal processing tools aimed at transforming a measured signal from time domain to angular domain. These techniques are applied to asynchronously sampled signals to obtain the same signal sampled at constant angular increments of a reference shaft. In some cases the outcome of the Order Tracking is directly the Fourier transform of such angular domain signal, whose frequency counterpart is defined as "order". Each order represents a fraction of the angular velocity of the reference shaft.
The spectrum of a chirp pulse describes its characteristics in terms of its frequency components. This frequency-domain representation is an alternative to the more familiar time-domain waveform, and the two versions are mathematically related by the Fourier transform.
The spectrum is of particular interest when pulses are subject to signal processing. For example, when a chirp pulse is compressed by its matched filter, the resulting waveform contains not only a main narrow pulse but, also, a variety of unwanted artifacts many of which are directly attributable to features in the chirp's spectral characteristics.
The simplest way to derive the spectrum of a chirp, now that computers are widely available, is to sample the time-domain waveform at a frequency well above the Nyquist limit and call up an FFT algorithm to obtain the desired result. As this approach was not an option for the early designers, they resorted to analytic analysis, where possible, or to graphical or approximation methods, otherwise. These early methods still remain helpful, however, as they give additional insight into the behavior and properties of chirps.














