Related Research Articles

Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros.
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples ("models") of algebraic structures. For instance, rather than take particular groups as the object of study, in universal algebra one takes the class of groups as an object of study.

In mathematics, complex geometry is the study of complex manifolds, complex algebraic varieties, and functions of several complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric aspects of complex analysis.
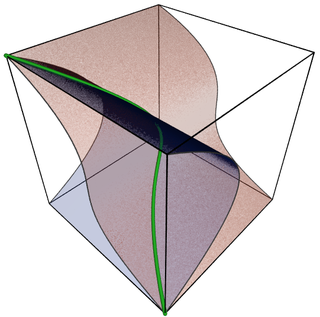
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.

In algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those operations defined for the integers. Ring theory studies the structure of rings, their representations, or, in different language, modules, special classes of rings, as well as an array of properties that proved to be of interest both within the theory itself and for its applications, such as homological properties and polynomial identities.

In mathematics, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symmetric spaces.
The concept of supergroup is a generalization of that of group. In other words, every supergroup carries a natural group structure, but there may be more than one way to structure a given group as a supergroup. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them. However the functions may have even and odd parts. Moreover, a supergroup has a super Lie algebra which plays a role similar to that of a Lie algebra for Lie groups in that they determine most of the representation theory and which is the starting point for classification.
In mathematics, a scheme is a mathematical structure that enlarges the notion of algebraic variety in several ways, such as taking account of multiplicities and allowing "varieties" defined over any commutative ring.

In mathematics, Diophantine geometry is the study of points of algebraic varieties with coordinates in the integers, rational numbers, and their generalizations. These generalizations typically are fields that are not algebraically closed, such as number fields, finite fields, function fields, and p-adic fields. It is a sub-branch of arithmetic geometry and is one approach to the theory of Diophantine equations, formulating questions about such equations in terms of algebraic geometry.
In mathematics, algebraic geometry and analytic geometry are two closely related subjects. While algebraic geometry studies algebraic varieties, analytic geometry deals with complex manifolds and the more general analytic spaces defined locally by the vanishing of analytic functions of several complex variables. The deep relation between these subjects has numerous applications in which algebraic techniques are applied to analytic spaces and analytic techniques to algebraic varieties.
Mathematics encompasses a growing variety and depth of subjects over history, and comprehension of it requires a system to categorize and organize these various subjects into a more general areas of mathematics. A number of different classification schemes have arisen, and though they share some similarities, there are differences due in part to the different purposes they serve.

In mathematics, arithmetic geometry is roughly the application of techniques from algebraic geometry to problems in number theory. Arithmetic geometry is centered around Diophantine geometry, the study of rational points of algebraic varieties.
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V. In classical algebraic geometry they are ratios of polynomials; in complex algebraic geometry these are meromorphic functions and their higher-dimensional analogues; in modern algebraic geometry they are elements of some quotient ring's field of fractions.
In algebraic geometry, a generic pointP of an algebraic variety X is, roughly speaking, a point at which all generic properties are true, a generic property being a property which is true for almost every point.

Geometry is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space that are related with distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a geometer.
S (Sundararaman) Ramanan is an Indian mathematician who works in the area of algebraic geometry, moduli spaces and Lie groups. He is one of India's leading mathematicians and recognised as an expert in algebraic geometry, especially in the area of moduli problems. He has also worked in differential geometry: his joint paper with MS Narasimhan on universal connections has been influential. It enabled SS Chern and B Simons to introduce what is known as the Chern-Simons invariant, which has proved useful in theoretical physics.
In algebraic geometry, Mnëv's universality theorem is a result which can be used to represent algebraic varieties as realizations of oriented matroids, a notion of combinatorics.
This is a glossary of algebraic geometry.
In mathematics, specifically in algebraic geometry, the fiber product of schemes is a fundamental construction. It has many interpretations and special cases. For example, the fiber product describes how an algebraic variety over one field determines a variety over a bigger field, or the pullback of a family of varieties, or a fiber of a family of varieties. Base change is a closely related notion.