Value restriction

Last updated February 02, 2023

In programming languages with Hindley-Milner type inference and imperative features, in particular the ML programming language family, the value restriction means that declarations are only polymorphically generalized if they are syntactic values (also called non-expansive). The value restriction prevents reference cells from holding values of different types and preserves type safety.

A Counter Example to Type Safety

In the Hindley–Milner type system, expressions can be given multiple types through parametric polymorphism. But naively giving multiple types to references breaks type safety. The following^[1] are typing rules for references and related operators in ML-like languages.

${\begin{aligned}{\mathtt {ref}}&:\forall \alpha .\alpha \to (\alpha \ {\mathtt {ref}})\\{\mathtt {!}}&:\forall \alpha .(\alpha \ {\mathtt {ref}})\to \alpha \\{\mathtt {:=}}&:\forall \alpha .(\alpha \ {\mathtt {ref}})\to \alpha \to {\mathtt {unit}}\end{aligned}}$

The operators have the following semantics: ${\textstyle {\mathtt {ref}}}$ takes a value and creates a reference containing that value, ${\textstyle {\mathtt {!}}}$ (dereference) takes a reference and reads the value in that reference, and ${\textstyle {\mathtt {:=}}}$ (assignment) updates a reference to contain a new value and returns a value of the unit type. Given these, the following program^[1] unsoundly applies a function meant for integers to a Boolean value.

letvalc=ref(fnx=>x)inc:=(fnx=>x+1);!ctrueend

The above program type checks using Hindley-Milner because c is given the type ${\textstyle \forall \alpha .(\alpha \to \alpha )\ {\mathtt {ref}}}$ , which is then instantiated to be of the type ${\textstyle ({\mathtt {int}}\to {\mathtt {int}})\ {\mathtt {ref}}}$ when typing the assignment c := (fn x => x + 1), and ${\textstyle ({\mathtt {bool}}\to {\mathtt {bool}})\ {\mathtt {ref}}}$ ref when typing the dereference !c true.

The Value Restriction

Under the value restriction, the types of let bound expressions are only generalized if the expressions are syntactic values. In his paper,^[1] Wright considers the following to be syntactic values: constants, variables, ${\textstyle \lambda }$ -expressions and constructors applied to values. The function and operator applications are not considered values. In particular, applications of the ${\mathtt {ref}}$ operator are not generalized. It is safe to generalize type variables of syntactic values because their evaluation cannot cause any side-effects such as writing to a reference.

The above example is rejected by the type checker under the value restriction as follows.

First c is given the type ${\textstyle (\alpha \to \alpha )\ {\mathtt {ref}}}$ . This type is not generalized and ${\textstyle \alpha }$ is a free variable in the typing context for the body of the let binding.
When the assignment is typed, the type of c is modified in the typing context to be of type ${\textstyle ({\mathtt {int}}\to {\mathtt {int}})\ {\mathtt {ref}}}$ via unification.
The dereference !c is typed as ${\mathtt {int}}\to {\mathtt {int}}$ , but is applied to a value of type ${\textstyle {\mathtt {bool}}}$ , and the type checker rejects the program.

Related Research Articles

ML is a general-purpose functional programming language. It is known for its use of the polymorphic Hindley–Milner type system, which automatically assigns the types of most expressions without requiring explicit type annotations, and ensures type safety – there is a formal proof that a well-typed ML program does not cause runtime type errors. ML provides pattern matching for function arguments, garbage collection, imperative programming, call-by-value and currying. It is used heavily in programming language research and is one of the few languages to be completely specified and verified using formal semantics. Its types and pattern matching make it well-suited and commonly used to operate on other formal languages, such as in compiler writing, automated theorem proving, and formal verification.

In computer programming, operator overloading, sometimes termed operator ad hoc polymorphism, is a specific case of polymorphism, where different operators have different implementations depending on their arguments. Operator overloading is generally defined by a programming language, a programmer, or both.

Standard ML (SML) is a general-purpose, modular, functional programming language with compile-time type checking and type inference. It is popular among compiler writers and programming language researchers, as well as in the development of theorem provers.

In computer programming, a type system is a logical system comprising a set of rules that assigns a property called a type to every "term". Usually the terms are various constructs of a computer program, such as variables, expressions, functions, or modules. A type system dictates the operations that can be performed on a term. For variables, the type system determines the allowed values of that term. Type systems formalize and enforce the otherwise implicit categories the programmer uses for algebraic data types, data structures, or other components.

Type inference refers to the automatic detection of the type of an expression in a formal language. These include programming languages and mathematical type systems, but also natural languages in some branches of computer science and linguistics.

In type theory, a typing rule is an inference rule that describes how a type system assigns a type to a syntactic construction. These rules may be applied by the type system to determine if a program is well-typed and what type expressions have. A prototypical example of the use of typing rules is in defining type inference in the simply typed lambda calculus, which is the internal language of Cartesian closed categories.

<span class="mw-page-title-main">ALGOL 68</span> Programming language

ALGOL 68 is an imperative programming language that was conceived as a successor to the ALGOL 60 programming language, designed with the goal of a much wider scope of application and more rigorously defined syntax and semantics.

System F is a typed lambda calculus that introduces, to simply typed lambda calculus, a mechanism of universal quantification over types. System F formalizes parametric polymorphism in programming languages, thus forming a theoretical basis for languages such as Haskell and ML. It was discovered independently by logician Jean-Yves Girard (1972) and computer scientist John C. Reynolds.

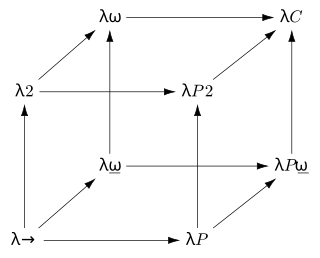
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:

In the C++ programming language, a reference is a simple reference datatype that is less powerful but safer than the pointer type inherited from C. The name C++ reference may cause confusion, as in computer science a reference is a general concept datatype, with pointers and C++ references being specific reference datatype implementations. The definition of a reference in C++ is such that it does not need to exist. It can be implemented as a new name for an existing object.

The simply typed lambda calculus, a form of type theory, is a typed interpretation of the lambda calculus with only one type constructor that builds function types. It is the canonical and simplest example of a typed lambda calculus. The simply typed lambda calculus was originally introduced by Alonzo Church in 1940 as an attempt to avoid paradoxical use of the untyped lambda calculus.

In computer programming languages, a recursive data type is a data type for values that may contain other values of the same type. Data of recursive types are usually viewed as directed graphs.

In programming languages and type theory, parametric polymorphism allows a single piece of code to be given a "generic" type, using variables in place of actual types, and then instantiated with particular types as needed. Parametrically polymorphic functions and data types are sometimes called generic functions and generic datatypes, respectively, and they form the basis of generic programming.

In computer science, a type class is a type system construct that supports ad hoc polymorphism. This is achieved by adding constraints to type variables in parametrically polymorphic types. Such a constraint typically involves a type class T and a type variable a, and means that a can only be instantiated to a type whose members support the overloaded operations associated with T.

ALGOL 68RS is the second ALGOL 68 compiler written by I. F. Currie and J. D. Morrison, at the Royal Signals and Radar Establishment (RSRE). Unlike the earlier ALGOL 68-R, it was designed to be portable, and implemented the language of the Revised Report.

In the area of mathematical logic and computer science known as type theory, a kind is the type of a type constructor or, less commonly, the type of a higher-order type operator. A kind system is essentially a simply typed lambda calculus "one level up", endowed with a primitive type, denoted $and called "type", which is the kind of any data type which does not need any type parameters.$

Q₀ is Peter Andrews' formulation of the simply-typed lambda calculus, and provides a foundation for mathematics comparable to first-order logic plus set theory. It is a form of higher-order logic and closely related to the logics of the HOL theorem prover family.

A Hindley–Milner (HM) type system is a classical type system for the lambda calculus with parametric polymorphism. It is also known as Damas–Milner or Damas–Hindley–Milner. It was first described by J. Roger Hindley and later rediscovered by Robin Milner. Luis Damas contributed a close formal analysis and proof of the method in his PhD thesis.

In mathematical logic, System U and System U⁻ are pure type systems, i.e. special forms of a typed lambda calculus with an arbitrary number of sorts, axioms and rules. They were both proved inconsistent by Jean-Yves Girard in 1972. This result led to the realization that Martin-Löf's original 1971 type theory was inconsistent as it allowed the same "Type in Type" behaviour that Girard's paradox exploits.

Flix is a functional, imperative, and logic programming language developed at Aarhus University, with funding from the Independent Research Fund Denmark, and by a community of open source contributors. The Flix language supports algebraic data types, pattern matching, parametric polymorphism, currying, higher-order functions, extensible records, channel and process-based concurrency, and tail call elimination. Two notable features of Flix are its type and effect system and its support for first-class Datalog constraints.

References

1 2 3 Wright, Andrew K. (1995-12-01). "Simple imperative polymorphism". LISP and Symbolic Computation. 8 (4): 343–355. doi:10.1007/BF01018828. ISSN 1573-0557. S2CID 19286877.

Mads Tofte (1988). Operational Semantics and Polymorphic Type Inference. PhD thesis.
M. Tofte (1990). "Type inference for polymorphic references".
O'Toole (1990). "Type Abstraction Rules for Reference: A Comparison of Four Which Have Achieved Notoriety".
Xavier Leroy & Pierre Weis (1991). "Polymorphic type inference and assignment". POPL '91.
A. K. Wright (1992). "Typing references by effect inference".
My Hoang, John C. Mitchell and Ramesh Viswanathan (1993). "Standard ML-NJ weak polymorphism and imperative constructs".
Andrew Wright (1995). "Simple imperative polymorphism". In LISP and Symbolic Computation , p. 343–356.
Jacques Garrigue (2004). "Relaxing the Value Restriction".

External links

Value Restriction — MLton
Notes on SML97's Value Restriction — Principles of Programming Languages, Geoffrey Smith, Florida International University

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 3 Wright, Andrew K. (1995-12-01). "Simple imperative polymorphism". LISP and Symbolic Computation. 8 (4): 343–355. doi:10.1007/BF01018828. ISSN 1573-0557. S2CID 19286877.

[1]