In physics, vector meson dominance (VMD) was a model developed by J. J. Sakurai [1] in the 1960s before the introduction of quantum chromodynamics to describe interactions between energetic photons and hadronic matter.
In particular, the hadronic components of the physical photon consist of the lightest vector mesons, , and . Therefore, interactions between photons and hadronic matter occur by the exchange of a hadron between the dressed photon and the hadronic target.
Measurements of the interaction between energetic photons and hadrons show that the interaction is much more intense than expected by the interaction of merely photons with the hadron's electric charge. Furthermore, the interaction of energetic photons with protons is similar to the interaction of photons with neutrons [2] in spite of the fact that the electric charge structures of protons and neutrons are substantially different.
According to VMD, the photon is a superposition of the pure electromagnetic photon (which interacts only with electric charges) and vector meson.
Just after 1970, when more accurate data on the above processes became available, some discrepancies with the VMD predictions appeared and new extensions of the model were published. [3] These theories are known as Generalized Vector Meson Dominance theories (GVMD).
Whilst the ultraviolet description of the standard model is based on QCD, work over many decades has involved writing a low energy effective description of QCD, and further, positing a possible "dual" description. One such popular description is that of the hidden local symmetry. [4] The dual description is based on the idea of emergence of gauge symmetries in the infrared of strongly coupled theories. Gauge symmetries are not really physical symmetries (only the global elements of the local gauge group are physical). This emergent property of gauge symmetries was demonstrated in Seiberg duality [5] and later in the development of the AdS/CFT correspondence. [6] In its generalised form, Vector Meson Dominance appears in AdS/CFT, AdS/QCD, AdS/condensed matter and some Seiberg dual constructions. It is therefore a common place idea within the theoretical physics community.
Measurements of the photon-hadron interactions in higher energy levels show that VMD cannot predict the interaction in such levels. In his Nobel lecture [7] J.I. Friedman summarizes the situation of VMD as follows: "...this eliminated the model [VMD] as a possible description of deep inelastic scattering... calculations of the generalized vector-dominance failed in general to describe the data over the full kinematic range..."
The Vector Meson Dominance model still sometimes makes significantly more accurate predictions of hadronic decays of excited light mesons involving photons than subsequent models such as the relativistic quark model for the meson wave function and the covariant oscillator quark model. [8] Similarly, the Vector Meson Dominance model has outperformed perturbative QCD in making predictions of transitional form factors of the neutral pion meson, the eta meson, and the eta prime meson, that are "hard to explain within QCD." [9] And, the model accurately reproduces recent experimental data for rho meson decays. [10] Generalizations of the Vector Meson Dominance model to higher energies, or to consider additional factors present in cases where VMD fails, have been proposed to address the shortcomings identified by Friedman and others. [11] [12]
A gluon is a type of elementary particle that mediates the strong interaction between quarks, acting as the exchange particle for the interaction. Gluons are massless vector bosons, thereby having a spin of 1. Through the strong interaction, gluons bind quarks into groups according to quantum chromodynamics (QCD), forming hadrons such as protons and neutrons.
A quark is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly observable matter is composed of up quarks, down quarks and electrons. Owing to a phenomenon known as color confinement, quarks are never found in isolation; they can be found only within hadrons, which include baryons and mesons, or in quark–gluon plasmas. For this reason, much of what is known about quarks has been drawn from observations of hadrons.
In theoretical physics, quantum chromodynamics (QCD) is the theory of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type of quantum field theory called a non-abelian gauge theory, with symmetry group SU(3). The QCD analog of electric charge is a property called color. Gluons are the force carriers of the theory, just as photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of particle physics. A large body of experimental evidence for QCD has been gathered over the years.
The Standard Model of particle physics is the theory describing three of the four known fundamental forces in the universe and classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.
The up quark or u quark is the lightest of all quarks, a type of elementary particle, and a significant constituent of matter. It, along with the down quark, forms the neutrons and protons of atomic nuclei. It is part of the first generation of matter, has an electric charge of +2/3 e and a bare mass of 2.2+0.5
−0.4 MeV/c2. Like all quarks, the up quark is an elementary fermion with spin 1/2, and experiences all four fundamental interactions: gravitation, electromagnetism, weak interactions, and strong interactions. The antiparticle of the up quark is the up antiquark, which differs from it only in that some of its properties, such as charge have equal magnitude but opposite sign.
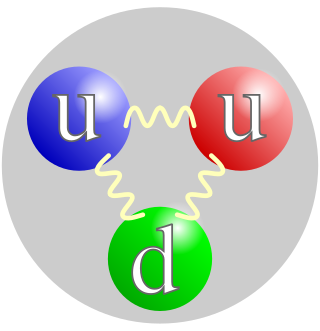
The down quark is a type of elementary particle, and a major constituent of matter. The down quark is the second-lightest of all quarks, and combines with other quarks to form composite particles called hadrons. Down quarks are most commonly found in atomic nuclei, where it combines with up quarks to form protons and neutrons. The proton is made of one down quark with two up quarks, and the neutron is made up of two down quarks with one up quark. Because they are found in every single known atom, down quarks are present in all everyday matter that we interact with.
The
J/ψ
(J/psi) meson is a subatomic particle, a flavor-neutral meson consisting of a charm quark and a charm antiquark. Mesons formed by a bound state of a charm quark and a charm anti-quark are generally known as "charmonium" or psions. The
J/ψ
is the most common form of charmonium, due to its spin of 1 and its low rest mass. The
J/ψ
has a rest mass of 3.0969 GeV/c2, just above that of the
η
c, and a mean lifetime of 7.2×10−21 s. This lifetime was about a thousand times longer than expected.
Hadronization is the process of the formation of hadrons out of quarks and gluons. There are two main branches of hadronization: quark-gluon plasma (QGP) transformation and colour string decay into hadrons. The transformation of quark-gluon plasma into hadrons is studied in lattice QCD numerical simulations, which are explored in relativistic heavy-ion experiments. Quark-gluon plasma hadronization occurred shortly after the Big Bang when the quark–gluon plasma cooled down to the Hagedorn temperature when free quarks and gluons cannot exist. In string breaking new hadrons are forming out of quarks, antiquarks and sometimes gluons, spontaneously created from the vacuum.
Two-photon physics, also called gamma–gamma physics, is a branch of particle physics that describes the interactions between two photons. Normally, beams of light pass through each other unperturbed. Inside an optical material, and if the intensity of the beams is high enough, the beams may affect each other through a variety of non-linear effects. In pure vacuum, some weak scattering of light by light exists as well. Also, above some threshold of this center-of-mass energy of the system of the two photons, matter can be created.
The QCD vacuum is the quantum vacuum state of quantum chromodynamics (QCD). It is an example of a non-perturbative vacuum state, characterized by non-vanishing condensates such as the gluon condensate and the quark condensate in the complete theory which includes quarks. The presence of these condensates characterizes the confined phase of quark matter.
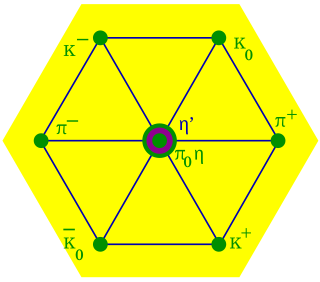
In particle physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks that give rise to the quantum numbers of the hadrons. The quark model underlies "flavor SU(3)", or the Eightfold Way, the successful classification scheme organizing the large number of lighter hadrons that were being discovered starting in the 1950s and continuing through the 1960s. It received experimental verification beginning in the late 1960s and is a valid effective classification of them to date. The model was independently proposed by physicists Murray Gell-Mann, who dubbed them "quarks" in a concise paper, and George Zweig, who suggested "aces" in a longer manuscript. André Petermann also touched upon the central ideas from 1963 to 1965, without as much quantitative substantiation. Today, the model has essentially been absorbed as a component of the established quantum field theory of strong and electroweak particle interactions, dubbed the Standard Model.
In quantum field theory, Seiberg duality, conjectured by Nathan Seiberg in 1994, is an S-duality relating two different supersymmetric QCDs. The two theories are not identical, but they agree at low energies. More precisely under a renormalization group flow they flow to the same IR fixed point, and so are in the same universality class. It is an extension to nonabelian gauge theories with N=1 supersymmetry of Montonen–Olive duality in N=4 theories and electromagnetic duality in abelian theories.
In particle physics, a rho meson is a short-lived hadronic particle that is an isospin triplet whose three states are denoted as
ρ+
,
ρ0
and
ρ−
. Along with pions and omega mesons, the rho meson carries the nuclear force within the atomic nucleus. After the pions and kaons, the rho mesons are the lightest strongly interacting particle, with a mass of 775.45±0.04 MeV for all three states.
In particle physics, the parton model is a model of hadrons, such as protons and neutrons, proposed by Richard Feynman. It is useful for interpreting the cascades of radiation produced from quantum chromodynamics (QCD) processes and interactions in high-energy particle collisions.
The J. J. Sakurai Prize for Theoretical Particle Physics, is presented by the American Physical Society at its annual April Meeting, and honors outstanding achievement in particle physics theory. The prize consists of a monetary award (US$10,000), a certificate citing the contributions recognized by the award, and a travel allowance for the recipient to attend the presentation. The award is endowed by the family and friends of particle physicist J. J. Sakurai. The prize has been awarded annually since 1985.
In strong interaction physics, light front holography or light front holographic QCD is an approximate version of the theory of quantum chromodynamics (QCD) which results from mapping the gauge theory of QCD to a higher-dimensional anti-de Sitter space (AdS) inspired by the AdS/CFT correspondence proposed for string theory. This procedure makes it possible to find analytic solutions in situations where strong coupling occurs, improving predictions of the masses of hadrons and their internal structure revealed by high-energy accelerator experiments. The most widely used approach to finding approximate solutions to the QCD equations, lattice QCD, has had many successful applications; however, it is a numerical approach formulated in Euclidean space rather than physical Minkowski space-time.
The photon structure function, in quantum field theory, describes the quark content of the photon. While the photon is a massless boson, through certain processes its energy can be converted into the mass of massive fermions. The function is defined by the process e + γ → e + hadrons. It is uniquely characterized by the linear increase in the logarithm of the electronic momentum transfer logQ2 and by the approximately linear rise in x, the fraction of the quark momenta within the photon. These characteristics are borne out by the experimental analyses of the photon structure function.
In theoretical particle physics, the gluon field is a four-vector field characterizing the propagation of gluons in the strong interaction between quarks. It plays the same role in quantum chromodynamics as the electromagnetic four-potential in quantum electrodynamics – the gluon field constructs the gluon field strength tensor.
The light-front quantization of quantum field theories provides a useful alternative to ordinary equal-time quantization. In particular, it can lead to a relativistic description of bound systems in terms of quantum-mechanical wave functions. The quantization is based on the choice of light-front coordinates, where plays the role of time and the corresponding spatial coordinate is . Here, is the ordinary time, is a Cartesian coordinate, and is the speed of light. The other two Cartesian coordinates, and , are untouched and often called transverse or perpendicular, denoted by symbols of the type . The choice of the frame of reference where the time and -axis are defined can be left unspecified in an exactly soluble relativistic theory, but in practical calculations some choices may be more suitable than others. The basic formalism is discussed elsewhere.
Stephan Narison is a Malagasy theoretical high-energy physicist specialized in quantum chromodynamics (QCD), the gauge theory of strong interactions. He is the founder of the Series of International Conferences in Quantum Chromodynamics (QCD-Montpellier) and of the Series of International Conferences in High-Energy Physics (HEPMAD-Madagascar).
