 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages) (Learn how and when to remove this template message)
|
In geometry, the positive and negative Voronoi poles of a cell in a Voronoi diagram are certain vertices of the diagram.
Let be the Voronoi diagram for a set of sites , and let be the Voronoi cell of corresponding to a site . If is bounded, then its positive pole is the vertex of the boundary of that has maximal distance to the point . If the cell is unbounded, then a positive pole is not defined.
Furthermore, let be the vector from to the positive pole, or, if the cell is unbounded, let be a vector in the average direction of all unbounded Voronoi edges of the cell. The negative pole is then the Voronoi vertex in with the largest distance to such that the vector and the vector from to make an angle larger than .
Here is the positive pole of and its negative. As the cell corresponding to is unbounded only the negative pole exists.
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 to e = 1.
In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several other superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces.
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane. For each seed there is a corresponding region consisting of all points of the plane closer to that seed than to any other. These regions are called Voronoi cells. The Voronoi diagram of a set of points is dual to its Delaunay triangulation.
In mathematics and physics, the centroid or geometric center of a plane figure is the arithmetic mean position of all the points in the figure. Informally, it is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin.
In mathematical physics, Minkowski space is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be an immediate consequence of the postulates of special relativity.
In mathematics, a quadratic form is a polynomial with terms all of degree two. For example,
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure of the degree to which the geometry of a given metric differs from that of ordinary Euclidean space or pseudo-Euclidean space.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional linear subspace σp of the tangent space at a point p of the manifold. It can be defined geometrically as the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a real-valued function on the 2-Grassmannian bundle over the manifold.
In geometry, a (general) conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex. Each of those lines is called a generatrix of the surface.
In mathematics, a vertex operator algebra (VOA) is an algebraic structure that plays an important role in two-dimensional conformal field theory and string theory. In addition to physical applications, vertex operator algebras have proven useful in purely mathematical contexts such as monstrous moonshine and the geometric Langlands correspondence.
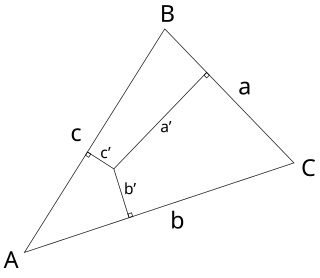
In geometry, the trilinear coordinatesx:y:z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x:y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y:z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z:x and vertices C and A.
In mathematics, specifically statistics and information geometry, a Bregman divergence or Bregman distance is a measure of distance between two points, defined in terms of a strictly convex function; they form an important class of divergences. When the points are interpreted as probability distributions – notably as either values of the parameter of a parametric model or as a data set of observed values – the resulting distance is a statistical distance. The most basic Bregman divergence is the squared Euclidean distance.
In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.
Fortune's algorithm is a sweep line algorithm for generating a Voronoi diagram from a set of points in a plane using O(n log n) time and O(n) space. It was originally published by Steven Fortune in 1986 in his paper "A sweepline algorithm for Voronoi diagrams."
In mathematics and theoretical physics, a pseudo-Euclidean space is a finite-dimensional real n-space together with a non-degenerate quadratic form q. Such a quadratic form can, given a suitable choice of basis (e1, ..., en), be applied to a vector x = x1e1 + … + xnen, giving
Mathematical diagrams, such as charts and graphs, are mainly designed to convey mathematical relationships—for example, comparisons over time.
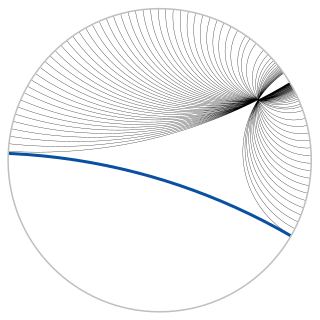
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which the points of the geometry are inside the unit disk, and the straight lines consist of all circular arcs contained within that disk that are orthogonal to the boundary of the disk, plus all diameters of the disk.
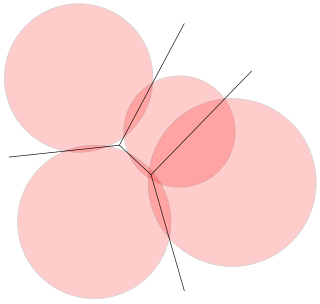
In computational geometry, a power diagram, also called a Laguerre–Voronoi diagram, Dirichlet cell complex, radical Voronoi tesselation or a sectional Dirichlet tesselation, is a partition of the Euclidean plane into polygonal cells defined from a set of circles. The cell for a given circle C consists of all the points for which the power distance to C is smaller than the power distance to the other circles. The power diagram is a form of generalized Voronoi diagram, and coincides with the Voronoi diagram of the circle centers in the case that all the circles have equal radii.
