WalkSAT

Last updated

In computer science, GSAT and WalkSAT are local search algorithms to solve Boolean satisfiability problems.

Both algorithms work on formulae in Boolean logic that are in, or have been converted into conjunctive normal form. They start by assigning a random value to each variable in the formula. If the assignment satisfies all clauses, the algorithm terminates, returning the assignment. Otherwise, a variable is flipped and the above is then repeated until all the clauses are satisfied. WalkSAT and GSAT differ in the methods used to select which variable to flip.

Both algorithms may restart with a new random assignment if no solution has been found for too long, as a way of getting out of local minima of numbers of unsatisfied clauses.

Many versions of GSAT and WalkSAT exist. WalkSAT has been proven particularly useful in solving satisfiability problems produced by conversion from automated planning problems. The approach to planning that converts planning problems into Boolean satisfiability problems is called satplan.

MaxWalkSAT is a variant of WalkSAT designed to solve the weighted satisfiability problem, in which each clause has associated with a weight, and the goal is to find an assignment—one which may or may not satisfy the entire formula—that maximizes the total weight of the clauses satisfied by that assignment.

Related Research Articles

In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.

Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint satisfaction methods. CSPs are the subject of research in both artificial intelligence and operations research, since the regularity in their formulation provides a common basis to analyze and solve problems of many seemingly unrelated families. CSPs often exhibit high complexity, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. Constraint programming (CP) is the field of research that specifically focuses on tackling these kinds of problems. Additionally, the Boolean satisfiability problem (SAT), satisfiability modulo theories (SMT), mixed integer programming (MIP) and answer set programming (ASP) are all fields of research focusing on the resolution of particular forms of the constraint satisfaction problem.

In computer science, local search is a heuristic method for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution maximizing a criterion among a number of candidate solutions. Local search algorithms move from solution to solution in the space of candidate solutions by applying local changes, until a solution deemed optimal is found or a time bound is elapsed.

In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time.

In computational complexity theory, the Cook–Levin theorem, also known as Cook's theorem, states that the Boolean satisfiability problem is NP-complete. That is, it is in NP, and any problem in NP can be reduced in polynomial time by a deterministic Turing machine to the Boolean satisfiability problem.

In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable or not. Horn-satisfiability and Horn clauses are named after Alfred Horn.

Bart Selman is a Dutch-American professor of computer science at Cornell University. He is also co-founder and principal investigator of the Center for Human-Compatible Artificial Intelligence (CHAI) at the University of California, Berkeley, led by Stuart J. Russell, and co-chair of the Computing Community Consortium's 20-year roadmap for AI research.

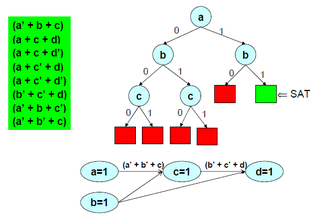
<span class="mw-page-title-main">DPLL algorithm</span> Type of search algorithm

In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem.

Satplan is a method for automated planning. It converts the planning problem instance into an instance of the Boolean satisfiability problem, which is then solved using a method for establishing satisfiability such as the DPLL algorithm or WalkSAT.

The Karloff–Zwick algorithm, in computational complexity theory, is a randomised approximation algorithm taking an instance of MAX-3SAT Boolean satisfiability problem as input. If the instance is satisfiable, then the expected weight of the assignment found is at least 7/8 of optimal. There is strong evidence that the algorithm achieves 7/8 of optimal even on unsatisfiable MAX-3SAT instances. Howard Karloff and Uri Zwick presented the algorithm in 1997.

MAX-3SAT is a problem in the computational complexity subfield of computer science. It generalises the Boolean satisfiability problem (SAT) which is a decision problem considered in complexity theory. It is defined as:

In computational complexity theory, the maximum satisfiability problem (MAX-SAT) is the problem of determining the maximum number of clauses, of a given Boolean formula in conjunctive normal form, that can be made true by an assignment of truth values to the variables of the formula. It is a generalization of the Boolean satisfiability problem, which asks whether there exists a truth assignment that makes all clauses true.

In computer science and mathematical logic, satisfiability modulo theories (SMT) is the problem of determining whether a mathematical formula is satisfiable. It generalizes the Boolean satisfiability problem (SAT) to more complex formulas involving real numbers, integers, and/or various data structures such as lists, arrays, bit vectors, and strings. The name is derived from the fact that these expressions are interpreted within ("modulo") a certain formal theory in first-order logic with equality. SMT solvers are tools that aim to solve the SMT problem for a practical subset of inputs. SMT solvers such as Z3 and cvc5 have been used as a building block for a wide range of applications across computer science, including in automated theorem proving, program analysis, program verification, and software testing.

In computer science and formal methods, a SAT solver is a computer program which aims to solve the Boolean satisfiability problem. On input a formula over Boolean variables, such as "(x or y) and (x or not y)", a SAT solver outputs whether the formula is satisfiable, meaning that there are possible values of x and y which make the formula true, or unsatisfiable, meaning that there are no such values of x and y. In this case, the formula is satisfiable when x is true, so the solver should return "satisfiable". Since the introduction of algorithms for SAT in the 1960s, modern SAT solvers have grown into complex software artifacts involving a large number of heuristics and program optimizations to work efficiently.

In theoretical computer science, the algorithmic Lovász local lemma gives an algorithmic way of constructing objects that obey a system of constraints with limited dependence.

MAXEkSAT is a problem in computational complexity theory that is a maximization version of the Boolean satisfiability problem 3SAT. In MAXEkSAT, each clause has exactly k literals, each with distinct variables, and is in conjunctive normal form. These are called k-CNF formulas. The problem is to determine the maximum number of clauses that can be satisfied by a truth assignment to the variables in the clauses.

In computer science, the Sharp Satisfiability Problem is the problem of counting the number of interpretations that satisfy a given Boolean formula, introduced by Valiant in 1979. In other words, it asks in how many ways the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. For example, the formula is satisfiable by three distinct boolean value assignments of the variables, namely, for any of the assignments, , and, we have

In computer science, conflict-driven clause learning (CDCL) is an algorithm for solving the Boolean satisfiability problem (SAT). Given a Boolean formula, the SAT problem asks for an assignment of variables so that the entire formula evaluates to true. The internal workings of CDCL SAT solvers were inspired by DPLL solvers. The main difference between CDCL and DPLL is that CDCL's backjumping is non-chronological.

The Boolean satisfiability problem can be stated formally as: given a Boolean expression with variables, finding an assignment of the variables such that is true. It is seen as the canonical NP-complete problem. While no efficient algorithm is known to solve this problem in the general case, there are certain heuristics, informally called 'rules of thumb' in programming, that can usually help solve the problem reasonably efficiently.

Algorithm selection is a meta-algorithmic technique to choose an algorithm from a portfolio on an instance-by-instance basis. It is motivated by the observation that on many practical problems, different algorithms have different performance characteristics. That is, while one algorithm performs well in some scenarios, it performs poorly in others and vice versa for another algorithm. If we can identify when to use which algorithm, we can optimize for each scenario and improve overall performance. This is what algorithm selection aims to do. The only prerequisite for applying algorithm selection techniques is that there exists a set of complementary algorithms.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.