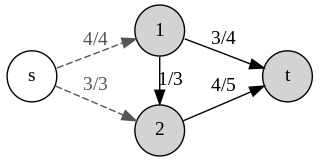
The subset sum problem (SSP) is a decision problem in computer science. In its most general formulation, there is a multiset of integers and a target-sum , and the question is to decide whether any subset of the integers sum to precisely . The problem is known to be NP-hard. Moreover, some restricted variants of it are NP-complete too, for example:
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.
In combinatorics, a greedoid is a type of set system. It arises from the notion of the matroid, which was originally introduced by Whitney in 1935 to study planar graphs and was later used by Edmonds to characterize a class of optimization problems that can be solved by greedy algorithms. Around 1980, Korte and Lovász introduced the greedoid to further generalize this characterization of greedy algorithms; hence the name greedoid. Besides mathematical optimization, greedoids have also been connected to graph theory, language theory, order theory, and other areas of mathematics.

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included. Antimatroids are commonly axiomatized in two equivalent ways, either as a set system modeling the possible states of such a process, or as a formal language modeling the different sequences in which elements may be included. Dilworth (1940) was the first to study antimatroids, using yet another axiomatization based on lattice theory, and they have been frequently rediscovered in other contexts.
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.
In theoretical computer science, a small-bias sample space is a probability distribution that fools parity functions. In other words, no parity function can distinguish between a small-bias sample space and the uniform distribution with high probability, and hence, small-bias sample spaces naturally give rise to pseudorandom generators for parity functions.
Samplesort is a sorting algorithm that is a divide and conquer algorithm often used in parallel processing systems. Conventional divide and conquer sorting algorithms partitions the array into sub-intervals or buckets. The buckets are then sorted individually and then concatenated together. However, if the array is non-uniformly distributed, the performance of these sorting algorithms can be significantly throttled. Samplesort addresses this issue by selecting a sample of size s from the n-element sequence, and determining the range of the buckets by sorting the sample and choosing p−1 < s elements from the result. These elements then divide the array into p approximately equal-sized buckets. Samplesort is described in the 1970 paper, "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W. D. Frazer and A. C. McKellar.
In mathematics, a packing in a hypergraph is a partition of the set of the hypergraph's edges into a number of disjoint subsets such that no pair of edges in each subset share any vertex. There are two famous algorithms to achieve asymptotically optimal packing in k-uniform hypergraphs. One of them is a random greedy algorithm which was proposed by Joel Spencer. He used a branching process to formally prove the optimal achievable bound under some side conditions. The other algorithm is called the Rödl nibble and was proposed by Vojtěch Rödl et al. They showed that the achievable packing by the Rödl nibble is in some sense close to that of the random greedy algorithm.
In combinatorial optimization, the matroid intersection problem is to find a largest common independent set in two matroids over the same ground set. If the elements of the matroid are assigned real weights, the weighted matroid intersection problem is to find a common independent set with the maximum possible weight. These problems generalize many problems in combinatorial optimization including finding maximum matchings and maximum weight matchings in bipartite graphs and finding arborescences in directed graphs.
The maximum coverage problem is a classical question in computer science, computational complexity theory, and operations research. It is a problem that is widely taught in approximation algorithms.
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.
The activity selection problem is a combinatorial optimization problem concerning the selection of non-conflicting activities to perform within a given time frame, given a set of activities each marked by a start time (si) and finish time (fi). The problem is to select the maximum number of activities that can be performed by a single person or machine, assuming that a person can only work on a single activity at a time. The activity selection problem is also known as the Interval scheduling maximization problem (ISMP), which is a special type of the more general Interval Scheduling problem.
In computer science and data mining, MinHash is a technique for quickly estimating how similar two sets are. The scheme was invented by Andrei Broder, and initially used in the AltaVista search engine to detect duplicate web pages and eliminate them from search results. It has also been applied in large-scale clustering problems, such as clustering documents by the similarity of their sets of words.
In mathematics, a submodular set function is a set function that, informally, describes the relationship between a set of inputs and an output, where adding more of one input has a decreasing additional benefit. The natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory and electrical networks. Recently, submodular functions have also found utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains.
In mathematics and computer science, a matroid oracle is a subroutine through which an algorithm may access a matroid, an abstract combinatorial structure that can be used to describe the linear dependencies between vectors in a vector space or the spanning trees of a graph, among other applications.
Matroid partitioning is a problem arising in the mathematical study of matroids and in the design and analysis of algorithms. Its goal is to partition the elements of a matroid into as few independent sets as possible. An example is the problem of computing the arboricity of an undirected graph, the minimum number of forests needed to cover all of its edges. Matroid partitioning may be solved in polynomial time, given an independence oracle for the matroid. It may be generalized to show that a matroid sum is itself a matroid, to provide an algorithm for computing ranks and independent sets in matroid sums, and to compute the largest common independent set in the intersection of two given matroids.
The distributional learning theory or learning of probability distribution is a framework in computational learning theory. It has been proposed from Michael Kearns, Yishay Mansour, Dana Ron, Ronitt Rubinfeld, Robert Schapire and Linda Sellie in 1994 and it was inspired from the PAC-framework introduced by Leslie Valiant.
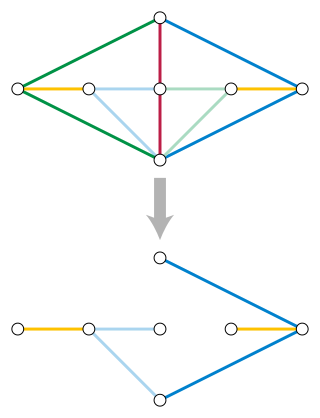
In combinatorial optimization, the matroid parity problem is a problem of finding the largest independent set of paired elements in a matroid. The problem was formulated by Lawler (1976) as a common generalization of graph matching and matroid intersection. It is also known as polymatroid matching, or the matchoid problem.
In mathematics, a basis of a matroid is a maximal independent set of the matroid—that is, an independent set that is not contained in any other independent set.
The welfare maximization problem is an optimization problem studied in economics and computer science. Its goal is to partition a set of items among agents with different utility functions, such that the welfare – defined as the sum of the agents' utilities – is as high as possible. In other words, the goal is to find an item allocation satisfying the utilitarian rule.















































