Minimax is a decision rule used in artificial intelligence, decision theory, game theory, statistics, and philosophy for minimizing the possible loss for a worst case scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.

In statistics, the logistic model is a statistical model that models the log-odds of an event as a linear combination of one or more independent variables. In regression analysis, logistic regression estimates the parameters of a logistic model. In binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable or a continuous variable. The corresponding probability of the value labeled "1" can vary between 0 and 1, hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. See § Background and § Definition for formal mathematics, and § Example for a worked example.
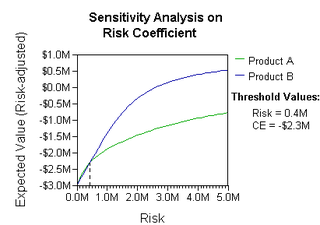
Multiple-criteria decision-making (MCDM) or multiple-criteria decision analysis (MCDA) is a sub-discipline of operations research that explicitly evaluates multiple conflicting criteria in decision making. It is also known as multiple attribute utility theory, multiple attribute value theory, multiple attribute preference theory, and multi-objective decision analysis.

Linear discriminant analysis (LDA), normal discriminant analysis (NDA), canonical variates analysis (CVA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification.

In statistics, the coefficient of determination, denoted R2 or r2 and pronounced "R squared", is the proportion of the variation in the dependent variable that is predictable from the independent variable(s).
In statistics, a generalized additive model (GAM) is a generalized linear model in which the linear response variable depends linearly on unknown smooth functions of some predictor variables, and interest focuses on inference about these smooth functions.
In statistics, unit-weighted regression is a simplified and robust version of multiple regression analysis where only the intercept term is estimated. That is, it fits a model
Pairwise comparison generally is any process of comparing entities in pairs to judge which of each entity is preferred, or has a greater amount of some quantitative property, or whether or not the two entities are identical. The method of pairwise comparison is used in the scientific study of preferences, attitudes, voting systems, social choice, public choice, requirements engineering and multiagent AI systems. In psychology literature, it is often referred to as paired comparison.
A decision matrix is a list of values in rows and columns that allows an analyst to systematically identify, analyze, and rate the performance of relationships between sets of values and information. Elements of a decision matrix show decisions based on certain decision criteria. The matrix is useful for looking at large masses of decision factors and assessing each factor's relative significance by weighting them by importance.
Segmented regression, also known as piecewise regression or broken-stick regression, is a method in regression analysis in which the independent variable is partitioned into intervals and a separate line segment is fit to each interval. Segmented regression analysis can also be performed on multivariate data by partitioning the various independent variables. Segmented regression is useful when the independent variables, clustered into different groups, exhibit different relationships between the variables in these regions. The boundaries between the segments are breakpoints.
Least absolute deviations (LAD), also known as least absolute errors (LAE), least absolute residuals (LAR), or least absolute values (LAV), is a statistical optimality criterion and a statistical optimization technique based on minimizing the sum of absolute deviations or the L1 norm of such values. It is analogous to the least squares technique, except that it is based on absolute values instead of squared values. It attempts to find a function which closely approximates a set of data by minimizing residuals between points generated by the function and corresponding data points. The LAD estimate also arises as the maximum likelihood estimate if the errors have a Laplace distribution. It was introduced in 1757 by Roger Joseph Boscovich.
The weighted product model (WPM) is a popular multi-criteria decision analysis (MCDA) / multi-criteria decision making (MCDM) method. It is similar to the weighted sum model (WSM) in that it produces a simple score, but has the very important advantage of overcoming the issue of 'adding apples and pears' i.e. adding together quantities measured in different units. While there are various ways of normalizing the data beforehand, the results of the weighted sum model differ according to which normalization is chosen. The weighted product approach does not require any normalization because it uses multiplication instead of addition to aggregate the data.
The decision-making paradox is a phenomenon related to decision-making and the quest for determining reliable decision-making methods. It was first described by Triantaphyllou, and has been recognized in the related literature as a fundamental paradox in multi-criteria decision analysis (MCDA), multi-criteria decision making (MCDM) and decision analysis since then.
Potentially All Pairwise RanKings of all possible Alternatives (PAPRIKA) is a method for multi-criteria decision making (MCDM) or conjoint analysis, as implemented by decision-making software and conjoint analysis products 1000minds and MeenyMo.
The Preference Ranking Organization METHod for Enrichment of Evaluations and its descriptive complement geometrical analysis for interactive aid are better known as the Promethee and Gaia methods.
In multiple criteria decision aiding (MCDA), multicriteria classification involves problems where a finite set of alternative actions should be assigned into a predefined set of preferentially ordered categories (classes). For example, credit analysts classify loan applications into risk categories, customers rate products and classify them into attractiveness groups, candidates for a job position are evaluated and their applications are approved or rejected, technical systems are prioritized for inspection on the basis of their failure risk, clinicians classify patients according to the extent to which they have a complex disease or not, etc.
In statistics, the focused information criterion (FIC) is a method for selecting the most appropriate model among a set of competitors for a given data set. Unlike most other model selection strategies, like the Akaike information criterion (AIC), the Bayesian information criterion (BIC) and the deviance information criterion (DIC), the FIC does not attempt to assess the overall fit of candidate models but focuses attention directly on the parameter of primary interest with the statistical analysis, say , for which competing models lead to different estimates, say for model . The FIC method consists in first developing an exact or approximate expression for the precision or quality of each estimator, say for , and then use data to estimate these precision measures, say . In the end the model with best estimated precision is selected. The FIC methodology was developed by Gerda Claeskens and Nils Lid Hjort, first in two 2003 discussion articles in Journal of the American Statistical Association and later on in other papers and in their 2008 book.
Inverse probability weighting is a statistical technique for estimating quantities related to a population other than the one from which the data was collected. Study designs with a disparate sampling population and population of target inference are common in application. There may be prohibitive factors barring researchers from directly sampling from the target population such as cost, time, or ethical concerns. A solution to this problem is to use an alternate design strategy, e.g. stratified sampling. Weighting, when correctly applied, can potentially improve the efficiency and reduce the bias of unweighted estimators.
The VIKOR method is a multi-criteria decision making (MCDM) method. It was originally developed by Serafim Opricovic in 1979 to solve decision problems with conflicting and noncommensurable criteria. It assumes that compromise is acceptable for conflict resolution and that the decision maker wants a solution that is the closest to the ideal, so the alternatives are evaluated according to all established criteria. VIKOR then ranks alternatives and determines the solution named compromise that is the closest to the ideal.

In statistics and data analysis, the application software SegReg is a free and user-friendly tool for linear segmented regression analysis to determine the breakpoint where the relation between the dependent variable and the independent variable changes abruptly.







