In computer science, especially model checking and abstract interpretation, widening refers to at least two different techniques in the analysis of abstract transition systems where infinite progressions of abstract states are replaced by a (computed or guessed [1] ) least fixed point. The use of the term in model checking is closely related to acceleration techniques, some authors reserving acceleration for exact computations. [2]
While many computer programs can be understood in terms of machine states and transitions (see formal semantics of programming languages), their state spaces may be too large to fully represent and analyse. Modern analysis techniques therefore try to reason about abstract states, which correspond to many concrete states.
Often, the abstract states are structured in such a way that by repeatedly following the effect of program steps or by coarsening the abstraction, one obtains a chain of abstractions that is proven to terminate.
Widening techniques and the closely related acceleration techniques are used in the forward analysis of systems in the discipline of symbolic model checking. The techniques detect cycles, i.e. sequences of abstract state transitions that could be repeated. When such a sequence can be repeated over and over, yielding new states (e.g. a variable might be incremented at every repetition), the symbolic analysis of the program will not explore all of these states in finite time. For several important families of systems such as pushdown systems, channel systems or counter systems, subclasses amenable to so-called flat acceleration have been identified [2] for which a complete analysis procedure exists that computes the whole set of reachable states. This type of forward analysis is also related to well structured transition systems, but well-structuredness alone is not sufficient for such procedures to be complete (for example, the coverability graph of a Petri net is always finite but in general, it overapproximates the true state space).
Cousot and Cousot [3] have introduced a notion of widening while defining the framework of abstract interpretation. An example for the widening of an abstract domain that appears in abstract interpretation [4] [5] would be replacing the upper bound of an interval by .
In mathematics and computer science, an algorithm is a finite sequence of mathematically rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use conditionals to divert the code execution through various routes and deduce valid inferences.
A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.
A programming language is a system of notation for writing computer programs. Programming languages are described in terms of their syntax (form) and semantics (meaning), usually defined by a formal language. Languages usually provide features such as a type system, variables, and mechanisms for error handling. An implementation of a programming language is required in order to execute programs, namely an interpreter or a compiler. An interpreter directly executes the source code, while a compiler produces an executable program.
In computer science, static program analysis is the analysis of computer programs performed without executing them, in contrast with dynamic program analysis, which is performed on programs during their execution in the integrated environment.
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algorithm.
In computer science, abstract interpretation is a theory of sound approximation of the semantics of computer programs, based on monotonic functions over ordered sets, especially lattices. It can be viewed as a partial execution of a computer program which gains information about its semantics without performing all the calculations.
In software engineering and computer science, abstraction is the process of generalizing concrete details, such as attributes, away from the study of objects and systems to focus attention on details of greater importance. Abstraction is a fundamental concept in computer science and software engineering, especially within the object-oriented programming paradigm. Examples of this include:
Structure and Interpretation of Computer Programs (SICP) is a computer science textbook by Massachusetts Institute of Technology professors Harold Abelson and Gerald Jay Sussman with Julie Sussman. It is known as the "Wizard Book" in hacker culture. It teaches fundamental principles of computer programming, including recursion, abstraction, modularity, and programming language design and implementation.
In computer science, formal methods are mathematically rigorous techniques for the specification, development, analysis, and verification of software and hardware systems. The use of formal methods for software and hardware design is motivated by the expectation that, as in other engineering disciplines, performing appropriate mathematical analysis can contribute to the reliability and robustness of a design.
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property, using formal methods of mathematics. Formal verification is a key incentive for formal specification of systems, and is at the core of formal methods. It represents an important dimension of analysis and verification in electronic design automation and is one approach to software verification. The use of formal verification enables the highest Evaluation Assurance Level (EAL7) in the framework of common criteria for computer security certification.
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification. This is typically associated with hardware or software systems, where the specification contains liveness requirements as well as safety requirements.
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science. The computability of a problem is closely linked to the existence of an algorithm to solve the problem.
Model-based testing is an application of model-based design for designing and optionally also executing artifacts to perform software testing or system testing. Models can be used to represent the desired behavior of a system under test (SUT), or to represent testing strategies and a test environment. The picture on the right depicts the former approach.
Algorithm characterizations are attempts to formalize the word algorithm. Algorithm does not have a generally accepted formal definition. Researchers are actively working on this problem. This article will present some of the "characterizations" of the notion of "algorithm" in more detail.
CADP is a toolbox for the design of communication protocols and distributed systems. CADP is developed by the CONVECS team at INRIA Rhone-Alpes and connected to various complementary tools. CADP is maintained, regularly improved, and used in many industrial projects.
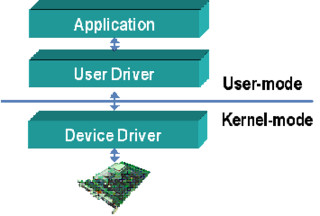
Device drivers are programs which allow software or higher-level computer programs to interact with a hardware device. These software components act as a link between the devices and the operating systems, communicating with each of these systems and executing commands. They provide an abstraction layer for the software above and also mediate the communication between the operating system kernel and the devices below.
Astrée is a static analyzer based on abstract interpretation. It analyzes programs written in the programming languages C and C++, and emits an exhaustive list of possible runtime errors and assertion violations. The defect classes covered include divisions by zero, buffer overflows, dereferences of null or dangling pointers, data races, deadlocks, etc. Astrée includes a static taint checker and helps finding cybersecurity vulnerabilities, such as Spectre. It is proprietary software written in the language OCaml.
Reachability is a fundamental problem that appears in several different contexts: finite- and infinite-state concurrent systems, computational models like cellular automata and Petri nets, program analysis, discrete and continuous systems, time critical systems, hybrid systems, rewriting systems, probabilistic and parametric systems, and open systems modelled as games.
Radhia Cousot was a French computer scientist known for inventing abstract interpretation.
Counterexample-guided abstraction refinement (CEGAR) is a technique for symbolic model checking. It is also applied in modal logic tableau calculi algorithms to optimise their efficiency.
