Structure and pseudocode
The face and vertex records are relatively simple, while the edge record is more complex.
- For each vertex, its record stores only the vertex's position (e.g. coordinates) and a reference to one incident edge. The other edges can be found by following further references in the edge.
- Similarly each face record only stores a reference to one of the edges surrounding the face. There is no need to store the direction of the edge relative to the face (CCW or CW) as the face can be trivially compared to the edge's own left and right faces to obtain this information.
- Finally, the structure of the edge record is as follows. An edge is assumed to be directed. The edge record contains two references to the vertices that make up the endpoints of the edge, two references to the faces on either side of the edge, and four references to the previous and next edges surrounding the left and right face.
In short, the edge record has references to all its adjacent records, both when traversing around an adjacent vertex or around an adjacent face.
class Edge { Vertex *vert_origin, *vert_destination; Face *face_left, *face_right; Edge *edge_left_cw, *edge_left_ccw, *edge_right_cw, *edge_right_ccw; } class Vertex { float x, y, z; Edge *edge; } class Face { Edge *edge; }
In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.

In vector computer graphics, CAD systems, and geographic information systems, geometric primitive is the simplest geometric shape that the system can handle. Sometimes the subroutines that draw the corresponding objects are called "geometric primitives" as well. The most "primitive" primitives are point and straight line segment, which were all that early vector graphics systems had.
The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data: computer graphics, geographic information systems (GIS), motion planning, and computer aided design (CAD).

In geometry, a disdyakis dodecahedron,, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it.

In 3D computer graphics and solid modeling, a polygon mesh is a collection of vertices, edges and faces that defines the shape of a polyhedral object. The faces usually consist of triangles, quadrilaterals (quads), or other simple convex polygons (n-gons), since this simplifies rendering, but may also be more generally composed of concave polygons, or even polygons with holes.
In 3D computer graphics, polygonal modeling is an approach for modeling objects by representing or approximating their surfaces using polygon meshes. Polygonal modeling is well suited to scanline rendering and is therefore the method of choice for real-time computer graphics. Alternate methods of representing 3D objects include NURBS surfaces, subdivision surfaces, and equation-based representations used in ray tracers.

Geometry processing, or mesh processing, is an area of research that uses concepts from applied mathematics, computer science and engineering to design efficient algorithms for the acquisition, reconstruction, analysis, manipulation, simulation and transmission of complex 3D models. As the name implies, many of the concepts, data structures, and algorithms are directly analogous to signal processing and image processing. For example, where image smoothing might convolve an intensity signal with a blur kernel formed using the Laplace operator, geometric smoothing might be achieved by convolving a surface geometry with a blur kernel formed using the Laplace-Beltrami operator.
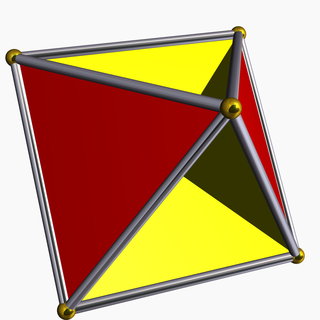
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 7 faces (4 triangles and 3 squares), 12 edges, and 6 vertices. Its vertex figure is a crossed quadrilateral. Its Coxeter–Dynkin diagram is (although this is a double covering of the tetrahemihexahedron).

In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.
A quad-edge data structure is a computer representation of the topology of a two-dimensional or three-dimensional map, that is, a graph drawn on a (closed) surface. It was first described by Jorge Stolfi and Leonidas J. Guibas. It is a variant of the earlier winged edge data structure.

In computer graphics, a triangle strip is a subset of triangles in a triangle mesh with shared vertices, and is a more memory-efficient method of storing information about the mesh. They are more efficient than un-indexed lists of triangles, but usually equally fast or slower than indexed triangle lists. The primary reason to use triangle strips is to reduce the amount of data needed to create a series of triangles. The number of vertices stored in memory is reduced from 3N to N + 2, where N is the number of triangles to be drawn. This allows for less use of disk space, as well as making them faster to load into RAM.

In computer graphics, a triangle mesh is a type of polygon mesh. It comprises a set of triangles that are connected by their common edges or vertices.
In geometry, a vertex is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.
The doubly connected edge list (DCEL), also known as half-edge data structure, is a data structure to represent an embedding of a planar graph in the plane, and polytopes in 3D. This data structure provides efficient manipulation of the topological information associated with the objects in question. It is used in many algorithms of computational geometry to handle polygonal subdivisions of the plane, commonly called planar straight-line graphs (PSLG). For example, a Voronoi diagram is commonly represented by a DCEL inside a bounding box.
In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope. In a polygon, an edge is a line segment on the boundary, and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces meet. A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.
A combinatorial map is a combinatorial representation of a graph on an orientable surface. A combinatorial map may also be called a combinatorial embedding, a rotation system, an orientable ribbon graph, a fat graph, or a cyclic graph. More generally, an -dimensional combinatorial map is a combinatorial representation of a graph on an -dimensional orientable manifold.
The Alexandrov uniqueness theorem is a rigidity theorem in mathematics, describing three-dimensional convex polyhedra in terms of the distances between points on their surfaces. It implies that convex polyhedra with distinct shapes from each other also have distinct metric spaces of surface distances, and it characterizes the metric spaces that come from the surface distances on polyhedra. It is named after Soviet mathematician Aleksandr Danilovich Aleksandrov, who published it in the 1940s.
In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.
In solid modeling and computer-aided design, the Euler operators modify the graph of connections to add or remove details of a mesh while preserving its topology. They are named by Baumgart after the Euler–Poincaré characteristic. He chose a set of operators sufficient to create useful meshes, some lose information and so are not invertible.










