
In physics, Kaluza–Klein theory is a classical unified field theory of gravitation and electromagnetism built around the idea of a fifth dimension beyond the common 4D of space and time and considered an important precursor to string theory. In their setup, the vacuum has the usual 3 dimensions of space and one dimension of time but with another microscopic extra spatial dimension in the shape of a tiny circle. Gunnar Nordström had an earlier, similar idea. But in that case, a fifth component was added to the electromagnetic vector potential, representing the Newtonian gravitational potential, and writing the Maxwell equations in five dimensions.
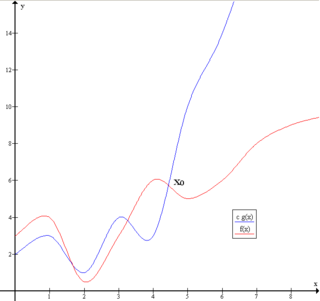
Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by German mathematicians Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for Ordnung, meaning the order of approximation.
In mathematics, the logarithmic integral function or integral logarithm li(x) is a special function. It is relevant in problems of physics and has number theoretic significance. In particular, according to the prime number theorem, it is a very good approximation to the prime-counting function, which is defined as the number of prime numbers less than or equal to a given value .
In computer science, the Akra–Bazzi method, or Akra–Bazzi theorem, is used to analyze the asymptotic behavior of the mathematical recurrences that appear in the analysis of divide and conquer algorithms where the sub-problems have substantially different sizes. It is a generalization of the master theorem for divide-and-conquer recurrences, which assumes that the sub-problems have equal size. It is named after mathematicians Mohamad Akra and Louay Bazzi.
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Aleksandr Lyapunov. In simple terms, if the solutions that start out near an equilibrium point stay near forever, then is Lyapunov stable. More strongly, if is Lyapunov stable and all solutions that start out near converge to , then is said to be asymptotically stable. The notion of exponential stability guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge. The idea of Lyapunov stability can be extended to infinite-dimensional manifolds, where it is known as structural stability, which concerns the behavior of different but "nearby" solutions to differential equations. Input-to-state stability (ISS) applies Lyapunov notions to systems with inputs.
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior.
In mathematics, an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular, often infinite, point. Investigations by Dingle (1973) revealed that the divergent part of an asymptotic expansion is latently meaningful, i.e. contains information about the exact value of the expanded function.

In theoretical physics, a Penrose diagram is a two-dimensional diagram capturing the causal relations between different points in spacetime through a conformal treatment of infinity. It is an extension of the Minkowski diagram of special relativity where the vertical dimension represents time, and the horizontal dimension represents a space dimension. Using this design, all light rays take a 45° path . Locally, the metric on a Penrose diagram is conformally equivalent to the metric of the spacetime depicted. The conformal factor is chosen such that the entire infinite spacetime is transformed into a Penrose diagram of finite size, with infinity on the boundary of the diagram. For spherically symmetric spacetimes, every point in the Penrose diagram corresponds to a 2-dimensional sphere .
In number theory, the Bateman–Horn conjecture is a statement concerning the frequency of prime numbers among the values of a system of polynomials, named after mathematicians Paul T. Bateman and Roger A. Horn who proposed it in 1962. It provides a vast generalization of such conjectures as the Hardy and Littlewood conjecture on the density of twin primes or their conjecture on primes of the form n2 + 1; it is also a strengthening of Schinzel's hypothesis H.
In statistics, the score test assesses constraints on statistical parameters based on the gradient of the likelihood function—known as the score—evaluated at the hypothesized parameter value under the null hypothesis. Intuitively, if the restricted estimator is near the maximum of the likelihood function, the score should not differ from zero by more than sampling error. While the finite sample distributions of score tests are generally unknown, they have an asymptotic χ2-distribution under the null hypothesis as first proved by C. R. Rao in 1948, a fact that can be used to determine statistical significance.
An asymptotically flat spacetime is a Lorentzian manifold in which, roughly speaking, the curvature vanishes at large distances from some region, so that at large distances, the geometry becomes indistinguishable from that of Minkowski spacetime.
Cointegration is a statistical property of a collection (X1, X2, ..., Xk) of time series variables. First, all of the series must be integrated of order d. Next, if a linear combination of this collection is integrated of order less than d, then the collection is said to be co-integrated. Formally, if (X,Y,Z) are each integrated of order d, and there exist coefficients a,b,c such that aX + bY + cZ is integrated of order less than d, then X, Y, and Z are cointegrated. Cointegration has become an important property in contemporary time series analysis. Time series often have trends—either deterministic or stochastic. In an influential paper, Charles Nelson and Charles Plosser (1982) provided statistical evidence that many US macroeconomic time series (like GNP, wages, employment, etc.) have stochastic trends.
The topological derivative is, conceptually, a derivative of a shape functional with respect to infinitesimal changes in its topology, such as adding an infinitesimal hole or crack. When used in higher dimensions than one, the term topological gradient is also used to name the first-order term of the topological asymptotic expansion, dealing only with infinitesimal singular domain perturbations. It has applications in shape optimization, topology optimization, image processing and mechanical modeling.
In statistical theory, a U-statistic is a class of statistics defined as the average over the application of a given function applied to all tuples of a fixed size. The letter "U" stands for unbiased. In elementary statistics, U-statistics arise naturally in producing minimum-variance unbiased estimators.
In probability theory, two sequences of probability measures are said to be contiguous if asymptotically they share the same support. Thus the notion of contiguity extends the concept of absolute continuity to the sequences of measures.
V-statistics are a class of statistics named for Richard von Mises who developed their asymptotic distribution theory in a fundamental paper in 1947. V-statistics are closely related to U-statistics introduced by Wassily Hoeffding in 1948. A V-statistic is a statistical function defined by a particular statistical functional of a probability distribution.
The 2014 Finnish Cup(Suomen Cup) is the 60th season of the Finnish Cup. 152 clubs entered the competition, including all sides on the top two levels of the Finnish football pyramid, 29 sides from Kakkonen and 101 from lower levels. The winner of the cup enters the qualifying rounds of the 2015–16 UEFA Europa League.
In metric geometry, asymptotic dimension of a metric space is a large-scale analog of Lebesgue covering dimension. The notion of asymptotic dimension was introduced by Mikhail Gromov in his 1993 monograph Asymptotic invariants of infinite groups in the context of geometric group theory, as a quasi-isometry invariant of finitely generated groups. As shown by Guoliang Yu, finitely generated groups of finite homotopy type with finite asymptotic dimension satisfy the Novikov conjecture. Asymptotic dimension has important applications in geometric analysis and index theory.
In gravitational theory, the Bondi–Metzner–Sachs (BMS) group, or the Bondi–Van der Burg–Metzner–Sachs group, is an asymptotic symmetry group of asymptotically flat, Lorentzian spacetimes at null infinity. It was originally formulated in 1962 by Hermann Bondi, M. G. Van der Burg, A. W. Metzner and Rainer K. Sachs in order to investigate the flow of energy at infinity due to propagating gravitational waves. Instead of the expected ordinary four spacetime translations of special relativity associated with the well-known conservation of momentum and energy, they found, much to their puzzling surprise, a novel infinite superset of direction-dependent time translations, which were named supertranslations. Half a century later, this work of Bondi, Van der Burg, Metzner, and Sachs is considered pioneering and seminal. In his autobiography, Bondi considered the 1962 work as his "best scientific work". The group of supertranslations is key to understanding the connections to quantum fields and gravitational wave memories.
Activation energy asymptotics (AEA), also known as large activation energy asymptotics, is an asymptotic analysis used in the combustion field utilizing the fact that the reaction rate is extremely sensitive to temperature changes due to the large activation energy of the chemical reaction.



