In computer science, an integer is a datum of integral data type, a data type that represents some range of mathematical integers. Integral data types may be of different sizes and may or may not be allowed to contain negative values. Integers are commonly represented in a computer as a group of binary digits (bits). The size of the grouping varies so the set of integer sizes available varies between different types of computers. Computer hardware nearly always provides a way to represent a processor register or memory address as an integer.
An order of magnitude is an approximation of the logarithm of a value relative to some contextually understood reference value, usually 10, interpreted as the base of the logarithm and the representative of values of magnitude one. Logarithmic distributions are common in nature and considering the order of magnitude of values sampled from such a distribution can be more intuitive. When the reference value is 10, the order of magnitude can be understood as the number of digits in the base-10 representation of the value. Similarly, if the reference value is one of some powers of 2, since computers store data in a binary format, the magnitude can be understood in terms of the amount of computer memory needed to store that value.
Large numbers are numbers significantly larger than those typically used in everyday life, appearing frequently in fields such as mathematics, cosmology, cryptography, and statistical mechanics. They are typically large positive integers, or more generally, large positive real numbers, but may also be other numbers in other contexts. Googology is the study of nomenclature and properties of large numbers.
The BMP file format or bitmap, is a raster graphics image file format used to store bitmap digital images, independently of the display device, especially on Microsoft Windows and OS/2 operating systems.
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976.
Conway chained arrow notation, created by mathematician John Horton Conway, is a means of expressing certain extremely large numbers. It is simply a finite sequence of positive integers separated by rightward arrows, e.g. .
In computer science, primitive data types are a set of basic data types from which all other data types are constructed. Specifically it often refers to the limited set of data representations in use by a particular processor, which all compiled programs must use. Most processors support a similar set of primitive data types, although the specific representations vary. More generally, "primitive data types" may refer to the standard data types built into a programming language. Data types which are not primitive are referred to as derived or composite.

A power of two is a number of the form 2n where n is an integer, that is, the result of exponentiation with number two as the base and integer n as the exponent.
64 (sixty-four) is the natural number following 63 and preceding 65.
Adler-32 is a checksum algorithm written by Mark Adler in 1995, modifying Fletcher's checksum. Compared to a cyclic redundancy check of the same length, it trades reliability for speed. Adler-32 is more reliable than Fletcher-16, and slightly less reliable than Fletcher-32.

In mathematics, tetration is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though and the left-exponent xb are common.
256 is the natural number following 255 and preceding 257.
IEC 61131-3 is the third part of the international standard IEC 61131 for programmable logic controllers. It was first published in December 1993 by the IEC; the current (third) edition was published in February 2013.
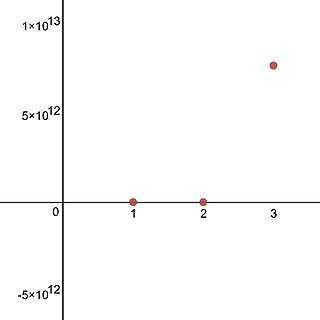
In mathematics, pentation is the fifth hyperoperation. Pentation is defined to be repeated tetration, similarly to how tetration is repeated exponentiation, exponentiation is repeated multiplication, and multiplication is repeated addition. The concept of "pentation" was named by English mathematician Reuben Goodstein in 1947, when he came up with the naming scheme for hyperoperations.
65535 is the integer after 65534 and before 65536.
60,000 (sixty thousand) is the natural number that comes after 59,999 and before 60,001. It is a round number. It is the value of (F25).
In number theory, a superperfect number is a positive integer n that satisfies
The number 4,294,967,295 is a whole number equal to 232 − 1. It is a perfect totient number, meaning it is equal to the sum of its iterated totients. It follows 4,294,967,294 and precedes 4,294,967,296. It has a factorization of .
In computer architecture, 16-bit integers, memory addresses, or other data units are those that are 16 bits wide. Also, 16-bit central processing unit (CPU) and arithmetic logic unit (ALU) architectures are those that are based on registers, address buses, or data buses of that size. 16-bit microcomputers are microcomputers that use 16-bit microprocessors.
















