
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number x to the base b is the exponent to which b must be raised, to produce x. For example, since 1000 = 103, the logarithm base 10 of 1000 is 3, or log10 (1000) = 3. The logarithm of x to base b is denoted as logb (x), or without parentheses, logb x, or even without the explicit base, log x, when no confusion is possible, or when the base does not matter such as in big O notation.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.
In calculus, the power rule is used to differentiate functions of the form , whenever is a real number. Since differentiation is a linear operation on the space of differentiable functions, polynomials can also be differentiated using this rule. The power rule underlies the Taylor series as it relates a power series with a function's derivatives.

In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of definite integrals.

François Viète, Seigneur de la Bigotière, commonly known by his mononym, Vieta, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to its innovative use of letters as parameters in equations. He was a lawyer by trade, and served as a privy councillor to both Henry III and Henry IV of France.

A Gabriel's horn is a type of geometric figure that has infinite surface area but finite volume. The name refers to the Christian tradition where the archangel Gabriel blows the horn to announce Judgment Day. The properties of this figure were first studied by Italian physicist and mathematician Evangelista Torricelli in the 17th century.

Bonaventura Francesco Cavalieri was an Italian mathematician and a Jesuate. He is known for his work on the problems of optics and motion, work on indivisibles, the precursors of infinitesimal calculus, and the introduction of logarithms to Italy. Cavalieri's principle in geometry partially anticipated integral calculus.
This is a list of logarithm topics, by Wikipedia page. See also the list of exponential topics.
Calculus, originally called infinitesimal calculus, is a mathematical discipline focused on limits, continuity, derivatives, integrals, and infinite series. Many elements of calculus appeared in ancient Greece, then in China and the Middle East, and still later again in medieval Europe and in India. Infinitesimal calculus was developed in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz independently of each other. An argument over priority led to the Leibniz–Newton calculus controversy which continued until the death of Leibniz in 1716. The development of calculus and its uses within the sciences have continued to the present day.

In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of xy = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation.

In linear algebra, a squeeze mapping, also called a squeeze transformation, is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a rotation or shear mapping.
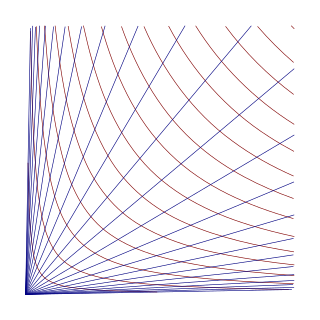
In mathematics, hyperbolic coordinates are a method of locating points in quadrant I of the Cartesian plane
In mathematics, quadrature is a historical term which means the process of determining area. This term is still used nowadays in the context of differential equations, where "solving an equation by quadrature" or "reduction to quadrature" means expressing its solution in terms of integrals.
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the nth polygon and the containing shape will become arbitrarily small as n becomes large. As this difference becomes arbitrarily small, the possible values for the area of the shape are systematically "exhausted" by the lower bound areas successively established by the sequence members.

Grégoire de Saint-Vincent - in Latin : Gregorius a Sancto Vincentio, in Dutch : Gregorius van St-Vincent - was a Flemish Jesuit and mathematician. He is remembered for his work on quadrature of the hyperbola.

Sant'Andrea delle Fratte is a 17th-century basilica church in Rome, Italy, dedicated to St. Andrew. The Cardinal Priest of the Titulus S. Andreae Apostoli de Hortis is Ennio Antonelli.

The history of logarithms is the story of a correspondence between multiplication on the positive real numbers and addition on the real number line that was formalized in seventeenth century Europe and was widely used to simplify calculation until the advent of the digital computer. The Napierian logarithms were published first in 1614. E. W. Hobson called it "one of the very greatest scientific discoveries that the world has seen." Henry Briggs introduced common logarithms, which were easier to use. Tables of logarithms were published in many forms over four centuries. The idea of logarithms was also used to construct the slide rule, which became ubiquitous in science and engineering until the 1970s. A breakthrough generating the natural logarithm was the result of a search for an expression of area against a rectangular hyperbola, and required the assimilation of a new function into standard mathematics.
A timeline of calculus and mathematical analysis.

In geometry, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfy the implicit equation In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length

In calculus, Cavalieri's quadrature formula, named for 17th-century Italian mathematician Bonaventura Cavalieri, is the integral
















