Related Research Articles

In probability theory and related fields, a stochastic or random process is a mathematical object usually defined as a family of random variables. Many stochastic processes can be represented by time series. However, a stochastic process is by nature continuous while a time series is a set of observations indexed by integers. A stochastic process may involve several related random variables.

Mathematical optimization or mathematical programming is the selection of a best element from some set of available alternatives. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
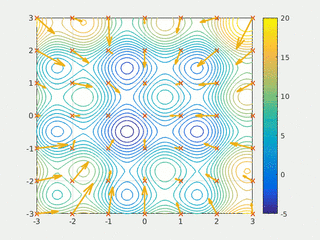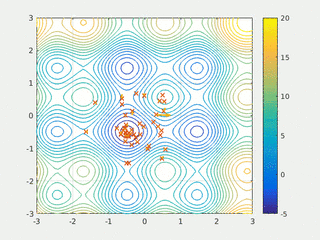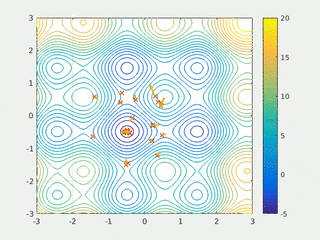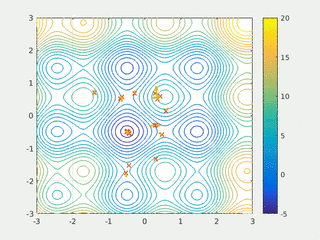
In computational science, particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formulae over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.
Global optimization is a branch of applied mathematics and numerical analysis that attempts to find the global minima or maxima of a function or a set of functions on a given set. It is usually described as a minimization problem because the maximization of the real-valued function is equivalent to the minimization of the function .

Sir David Roxbee Cox is a prominent British statistician.
Peter Whittle is a mathematician and statistician from New Zealand, working in the fields of stochastic nets, optimal control, time series analysis, stochastic optimisation and stochastic dynamics. From 1967 to 1994, he was the Churchill Professor of Mathematics for Operational Research at the University of Cambridge.
Stochastic diffusion search (SDS) was first described in 1989 as a population-based, pattern-matching algorithm [Bishop, 1989]. It belongs to a family of swarm intelligence and naturally inspired search and optimisation algorithms which includes ant colony optimization, particle swarm optimization and genetic algorithms; as such SDS was the first Swarm Intelligence metaheuristic. Unlike stigmergetic communication employed in ant colony optimization, which is based on modification of the physical properties of a simulated environment, SDS uses a form of direct (one-to-one) communication between the agents similar to the tandem calling mechanism employed by one species of ants, Leptothorax acervorum.
Stochastic optimization (SO) methods are optimization methods that generate and use random variables. For stochastic problems, the random variables appear in the formulation of the optimization problem itself, which involves random objective functions or random constraints. Stochastic optimization methods also include methods with random iterates. Some stochastic optimization methods use random iterates to solve stochastic problems, combining both meanings of stochastic optimization. Stochastic optimization methods generalize deterministic methods for deterministic problems.

In time series analysis, singular spectrum analysis (SSA) is a nonparametric spectral estimation method. It combines elements of classical time series analysis, multivariate statistics, multivariate geometry, dynamical systems and signal processing. Its roots lie in the classical Karhunen (1946)–Loève spectral decomposition of time series and random fields and in the Mañé (1981)–Takens (1981) embedding theorem. SSA can be an aid in the decomposition of time series into a sum of components, each having a meaningful interpretation. The name "singular spectrum analysis" relates to the spectrum of eigenvalues in a singular value decomposition of a covariance matrix, and not directly to a frequency domain decomposition.
In game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. More specifically, a state variable or variables evolve over time according to a differential equation. Early analyses reflected military interests, considering two actors—the pursuer and the evader—with diametrically opposed goals. More recent analyses have reflected engineering or economic considerations.
Jan Hendrik van Schuppen is a Dutch mathematician and Professor at the Department of Mathematics of the Vrije Universiteit, known for his contributions in the field of systems theory, particularly on control theory and system identification, on probability, and on a number of related practical applications.

Dimitri Panteli Bertsekas is an applied mathematician, electrical engineer, and computer scientist, a McAfee Professor at the Department of Electrical Engineering and Computer Science in School of Engineering at the Massachusetts Institute of Technology (MIT), Cambridge, Massachusetts, and also a Fulton Professor of Computational Decision Making at Arizona State University, Tempe.
Roger Jean-Baptiste Robert Wets is a "pioneer" in stochastic programming and a leader in variational analysis who publishes as Roger J-B Wets. His research, expositions, graduate students, and his collaboration with R. Tyrrell Rockafellar have had a profound influence on optimization theory, computations, and applications. Since 2009, Wets has been a distinguished research professor at the mathematics department of the University of California, Davis.

Sergio Albeverio is a Swiss mathematician and mathematical physicist working in numerous fields of mathematics and its applications. In particular he is known for his work in probability theory, analysis, mathematical physics, and in the areas algebra, geometry, number theory, as well as in applications, from natural to social-economic sciences.
Mark Herbert Ainsworth Davis (1945–2020) was Professor of Mathematics at Imperial College London. He made fundamental contributions to the theory of stochastic processes, stochastic control and mathematical finance.

Leon Petrosjan is a professor of Applied Mathematics and the Head of the Department of Mathematical Game theory and Statistical Decision Theory at the St. Petersburg University, Russia.
Institute of Mathematics of the National Academy of Sciences of Ukraine is a government-owned research institute in Ukraine that carries out basic research and trains highly qualified professionals in the field of mathematics. It was founded on 13 February 1934.

Darinka Dentcheva is a Bulgarian-American mathematician, noted for her contributions to convex analysis, stochastic programming, and risk-averse optimization.
Masanao Aoki was a Japanese engineer and economist. He was a Professor emeritus of Economics at University of California, Los Angeles.
Vivek Shripad Borkar is an Indian electrical engineer, mathematician and an Institute chair professor at the Indian Institute of Technology, Mumbai. He is known for introducing analytical paradigm in stochastic optimal control processes and is an elected fellow of all the three major Indian science academies viz. the Indian Academy of Sciences, Indian National Science Academy and the National Academy of Sciences, India. He also holds elected fellowships of The World Academy of Sciences, Institute of Electrical and Electronics Engineers, Indian National Academy of Engineering and the American Mathematical Society. The Council of Scientific and Industrial Research, the apex agency of the Government of India for scientific research, awarded him the Shanti Swarup Bhatnagar Prize for Science and Technology, one of the highest Indian science awards for his contributions to Engineering Sciences in 1992. He received the TWAS Prize of the World Academy of Sciences in 2009.
References
- ↑ Google Scholar
- ↑ Cardiff University
- ↑ Centre for Optimisation and its Applications
- ↑ Theory of Global Random Search, Springer, 1991
- ↑ Stochastic Global Optimization, Springer, 2008
- ↑ Analysis of time series structure, Chapman and Hall, 1991
- ↑ Dynamical Search, Chapman and Hall, 1999
- ↑ Singular Spectrum Analysis for Time Series, Springer, 2013
- ↑ JASA
- ↑ Stochastic Global Optimization - Springer (Reviews)
- ↑ Cardiff University
- ↑ Society for Global Optimization
- ↑ AMS Notices