Related Research Articles

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering.

In mathematics, a partial differential equation (PDE) is an equation which computes a function between various partial derivatives of a multivariable function.
Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).
In numerical analysis, a multigrid method is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners.

Louis Nirenberg was a Canadian-American mathematician, considered one of the most outstanding mathematicians of the 20th century.
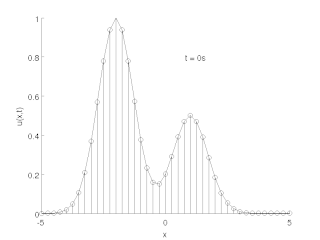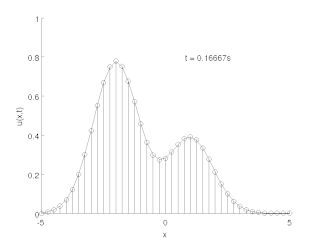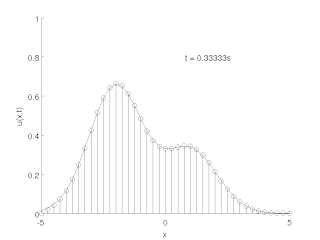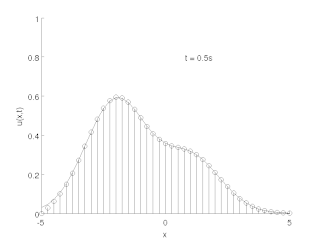
The method of lines is a technique for solving partial differential equations (PDEs) in which all but one dimension is discretized. By reducing a PDE to a single continuous dimension, the method of lines allows solutions to be computed via methods and software developed for the numerical integration of ordinary differential equations (ODEs) and differential-algebraic systems of equations (DAEs). Many integration routines have been developed over the years in many different programming languages, and some have been published as open source resources.
Christopher John Budd is a British mathematician known especially for his contribution to non-linear differential equations and their applications in industry. He is currently Professor of Applied Mathematics at the University of Bath, and was Professor of Geometry at Gresham College from 2016 to 2020.
In mathematics, in particular numerical analysis, the FETI method is an iterative substructuring method for solving systems of linear equations from the finite element method for the solution of elliptic partial differential equations, in particular in computational mechanics In each iteration, FETI requires the solution of a Neumann problem in each substructure and the solution of a coarse problem. The simplest version of FETI with no preconditioner in the substructure is scalable with the number of substructures but the condition number grows polynomially with the number of elements per substructure. FETI with a preconditioner consisting of the solution of a Dirichlet problem in each substructure is scalable with the number of substructures and its condition number grows only polylogarithmically with the number of elements per substructure. The coarse space in FETI consists of the nullspace on each substructure.
In mathematics, the Schwarz alternating method or alternating process is an iterative method introduced in 1869–1870 by Hermann Schwarz in the theory of conformal mapping. Given two overlapping regions in the complex plane in each of which the Dirichlet problem could be solved, Schwarz described an iterative method for solving the Dirichlet problem in their union, provided their intersection was suitably well behaved. This was one of several constructive techniques of conformal mapping developed by Schwarz as a contribution to the problem of uniformization, posed by Riemann in the 1850s and first resolved rigorously by Koebe and Poincaré in 1907. It furnished a scheme for uniformizing the union of two regions knowing how to uniformize each of them separately, provided their intersection was topologically a disk or an annulus. From 1870 onwards Carl Neumann also contributed to this theory.

Jinchao Xu is an American-Chinese mathematician. He is currently the Verne M. Willaman Professor in the Department of Mathematics at the Pennsylvania State University, University Park. He is known for his work on multigrid methods, domain decomposition methods, finite element methods, and more recently deep neural networks.
In mathematics, a Poincaré–Steklov operator maps the values of one boundary condition of the solution of an elliptic partial differential equation in a domain to the values of another boundary condition. Usually, either of the boundary conditions determines the solution. Thus, a Poincaré–Steklov operator encapsulates the boundary response of the system modelled by the partial differential equation. When the partial differential equation is discretized, for example by finite elements or finite differences, the discretization of the Poincaré–Steklov operator is the Schur complement obtained by eliminating all degrees of freedom inside the domain.

Annalisa Buffa is an Italian mathematician, specializing in numerical analysis and partial differential equations (PDE). She is a professor of mathematics at EPFL and holds the Chair of Numerical Modeling and Simulation.

Geneviève Raugel was a French mathematician working in the field of numerical analysis and dynamical systems.
Christoph Schwab is a German applied mathematician, specializing in numerical analysis of partial differential equations and boundary integral equations.
Angela Kunoth is a German mathematician specializing in the numerical analysis of partial differential equations. She is a professor of mathematics at the University of Cologne, and the editor-in-chief of SIAM Journal on Numerical Analysis.
Monique Dauge is a French mathematician and numerical analyst specializing in partial differential equations, spectral theory, and applications to scientific computing. She is an emeritus senior researcher at the French National Centre for Scientific Research (CNRS), associated with the University of Rennes 1.
Alison Ramage is a British applied mathematician and numerical analyst specialising in preconditioning methods for numerical linear algebra, and their applications to the numerical solution of partial differential equations. She is a reader in the Department of Mathematics and Statistics at the University of Strathclyde.

Klaus Schmitt is an American mathematician doing research in nonlinear differential equations, and nonlinear analysis.
Paola F. Antonietti is an Italian applied mathematician and numerical analyst whose research concerns numerical methods for partial differential equations, and particularly domain decomposition methods, with applications in scientific computing and Applied Sciences such as the computational modelling of neurodegenerative disorders and simulating the propagation of seismic waves. She is Professor of Numerical Analysis at the Polytechnic University of Milan.
References
- 1 2 3 Mihai, Loredana Angela (2005), "A class of alternate strip-based domain decomposition methods for elliptic partial differential Equations", Durham e-Theses (Doctoral), Durham University; see Acknowledgements, p. v
- 1 2 3 "Angela Mihai", Profiles, Cardiff University, retrieved 2023-08-02
- ↑ Mathematicians propose new model to quantify materials uncertainties, Cardiff University, 16 April 2019, retrieved 2023-08-02
- ↑ Angela Mihai at the Mathematics Genealogy Project
- ↑ Dr Angela Mihai elected Vice President of SIAM-UKIE, Cardiff University, 24 May 2023, retrieved 2023-08-02