
In the mathematical field of topology, a homeomorphism, also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.
In differential geometry, the Atiyah–Singer index theorem, proved by Michael Atiyah and Isadore Singer (1963), states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index. It includes many other theorems, such as the Chern–Gauss–Bonnet theorem and Riemann–Roch theorem, as special cases, and has applications to theoretical physics.

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group. These concepts are named after the mathematician J. H. C. Whitehead.
In mathematics, an n-dimensional differential structure on a set M makes M into an n-dimensional differential manifold, which is a topological manifold with some additional structure that allows for differential calculus on the manifold. If M is already a topological manifold, it is required that the new topology be identical to the existing one.
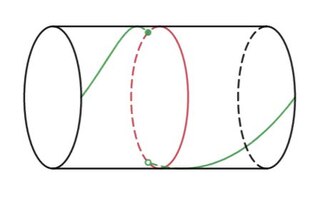
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface.
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.

In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In mathematics, a 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different. There exist some topological 4-manifolds which admit no smooth structure, and even if there exists a smooth structure, it need not be unique.

In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.
In topology, a branch of mathematics, a topological manifold is a topological space that locally resembles real n-dimensional Euclidean space. Topological manifolds are an important class of topological spaces, with applications throughout mathematics. All manifolds are topological manifolds by definition. Other types of manifolds are formed by adding structure to a topological manifold. Every manifold has an "underlying" topological manifold, obtained by simply "forgetting" the added structure. However, not every topological manifold can be endowed with a particular additional structure. For example, the E8 manifold is a topological manifold which cannot be endowed with a differentiable structure.
In mathematics, a piecewise linear (PL) manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions. This is slightly stronger than the topological notion of a triangulation.
The Hauptvermutung of geometric topology is a now refuted conjecture asking whether any two triangulations of a triangulable space have subdivisions that are combinatorially equivalent, i.e. the subdivided triangulations are built up in the same combinatorial pattern. It was originally formulated as a conjecture in 1908 by Ernst Steinitz and Heinrich Franz Friedrich Tietze, but it is now known to be false.
In mathematics, more specifically in geometric topology, the Kirby–Siebenmann class is an obstruction for topological manifolds to allow a PL-structure.

Robion Cromwell Kirby is a Professor of Mathematics at the University of California, Berkeley who specializes in low-dimensional topology. Together with Laurent C. Siebenmann he developed the Kirby–Siebenmann invariant for classifying the piecewise linear structures on a topological manifold. He also proved the fundamental result on the Kirby calculus, a method for describing 3-manifolds and smooth 4-manifolds by surgery on framed links. Along with his significant mathematical contributions, he has over 50 doctoral students and is the editor of an influential problem list.
In 4-dimensional topology, a branch of mathematics, Rokhlin's theorem states that if a smooth, orientable, closed 4-manifold M has a spin structure, then the signature of its intersection form, a quadratic form on the second cohomology group , is divisible by 16. The theorem is named for Vladimir Rokhlin, who proved it in 1952.

Laurent Carl Siebenmann is a Canadian mathematician based at the Université de Paris-Sud at Orsay, France.
In mathematics, a microbundle is a generalization of the concept of vector bundle, introduced by the American mathematician John Milnor in 1964. It allows the creation of bundle-like objects in situations where they would not ordinarily be thought to exist. For example, the tangent bundle is defined for a smooth manifold but not a topological manifold; use of microbundles allows the definition of a topological tangent bundle.
Wu-Chung Hsiang is a Chinese-American mathematician, specializing in topology. Hsiang served as chairman of the Department of Mathematics at Princeton University from 1982 to 1985 and was one of the most influential topologists of the second half of the 20th century.










