Related Research Articles

APL is a programming language developed in the 1960s by Kenneth E. Iverson. Its central datatype is the multidimensional array. It uses a large range of special graphic symbols to represent most functions and operators, leading to very concise code. It has been an important influence on the development of concept modeling, spreadsheets, functional programming, and computer math packages. It has also inspired several other programming languages.

In mathematics, a binary operation or dyadic operation is a rule for combining two elements to produce another element. More formally, a binary operation is an operation of arity two.

MATLAB is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages.

GNU Octave is a scientific programming language for scientific computing and numerical computation. Octave helps in solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB. It may also be used as a batch-oriented language. As part of the GNU Project, it is free software under the terms of the GNU General Public License.
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal matrix is , while an example of a 3×3 diagonal matrix is. An identity matrix of any size, or any multiple of it is a diagonal matrix called scalar matrix, for example, . In geometry, a diagonal matrix may be used as a scaling matrix, since matrix multiplication with it results in changing scale (size) and possibly also shape; only a scalar matrix results in uniform change in scale.
In mathematics, an algebra over a field is a vector space equipped with a bilinear product. Thus, an algebra is an algebraic structure consisting of a set together with operations of multiplication and addition and scalar multiplication by elements of a field and satisfying the axioms implied by "vector space" and "bilinear".
Perl Data Language is a set of free software array programming extensions to the Perl programming language. PDL extends the data structures built into Perl, to include large multidimensional arrays, and adds functionality to manipulate those arrays as vector objects. It also provides tools for image processing, machine learning, computer modeling of physical systems, and graphical plotting and presentation. Simple operations are automatically vectorized across complete arrays, and higher-dimensional operations are supported.
Basic Linear Algebra Subprograms (BLAS) is a specification that prescribes a set of low-level routines for performing common linear algebra operations such as vector addition, scalar multiplication, dot products, linear combinations, and matrix multiplication. They are the de facto standard low-level routines for linear algebra libraries; the routines have bindings for both C and Fortran. Although the BLAS specification is general, BLAS implementations are often optimized for speed on a particular machine, so using them can bring substantial performance benefits. BLAS implementations will take advantage of special floating point hardware such as vector registers or SIMD instructions.

In computing, row-major order and column-major order are methods for storing multidimensional arrays in linear storage such as random access memory.
The programming language APL is distinctive in being symbolic rather than lexical: its primitives are denoted by symbols, not words. These symbols were originally devised as a mathematical notation to describe algorithms. APL programmers often assign informal names when discussing functions and operators but the core functions and operators provided by the language are denoted by non-textual symbols.

In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a vector. Specifically, the vectorization of a m × n matrix A, denoted vec(A), is the mn × 1 column vector obtained by stacking the columns of the matrix A on top of one another:
In computer programming, a scientific programming language can refer to two degrees of the same concept.
The TomSym MATLAB symbolic modeling engine is a platform for modeling applied optimization and optimal control problems.

Pure, successor to the equational language Q, is a dynamically typed, functional programming language based on term rewriting. It has facilities for user-defined operator syntax, macros, arbitrary-precision arithmetic, and compiling to native code through the LLVM. Pure is free and open-source software distributed (mostly) under the GNU Lesser General Public License version 3 or later.

In mathematics, a matrix is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object.
In computer science, array is a data type that represents a collection of elements, each selected by one or more indices that can be computed at run time during program execution. Such a collection is usually called an array variable or array value. By analogy with the mathematical concepts vector and matrix, array types with one and two indices are often called vector type and matrix type, respectively. More generally, a multidimensional array type can be called a tensor type, by analogy with the physical concept, tensor.
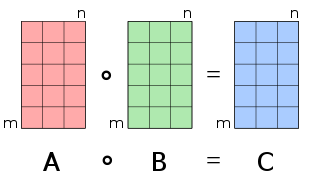
In mathematics, the Hadamard product is a binary operation that takes in two matrices of the same dimensions and returns a matrix of the multiplied corresponding elements. This operation can be thought as a "naive matrix multiplication" and is different from the matrix product. It is attributed to, and named after, either French mathematician Jacques Hadamard or German mathematician Issai Schur.

GraphBLAS is an API specification that defines standard building blocks for graph algorithms in the language of linear algebra. GraphBLAS is built upon the notion that a sparse matrix can be used to represent graphs as either an adjacency matrix or an incidence matrix. The GraphBLAS specification describes how graph operations can be efficiently implemented via linear algebraic methods over different semirings.
References
- ↑ Stéfan van der Walt; S. Chris Colbert & Gaël Varoquaux (2011). "The NumPy array: a structure for efficient numerical computation". Computing in Science and Engineering. IEEE. 13 (2): 22–30. arXiv: 1102.1523 . Bibcode:2011CSE....13b..22V. doi:10.1109/mcse.2011.37. S2CID 16907816.
- ↑ Iverson, K. E. (1980). "Notation as a Tool of Thought". Communications of the ACM. 23 (8): 444–465. doi: 10.1145/358896.358899 .
- ↑ Surana P (2006). Meta-Compilation of Language Abstractions (Thesis).
- ↑ Kuketayev. "The Data Abstraction Penalty (DAP) Benchmark for Small Objects in Java". Archived from the original on 2009-01-11. Retrieved 2008-03-17.
- ↑ Chatzigeorgiou; Stephanides (2002). "Evaluating Performance and Power Of Object-Oriented Vs. Procedural Programming Languages". In Blieberger; Strohmeier (eds.). Proceedings - 7th International Conference on Reliable Software Technologies - Ada-Europe'2002. Springer. p. 367. ISBN 978-3-540-43784-0.
- ↑ Ada Reference Manual: G.3.1 Real Vectors and Matrices
- ↑ "GNU Octave Manual. Arithmetic Operators" . Retrieved 2011-03-19.
- ↑ "MATLAB documentation. Arithmetic Operators". Archived from the original on 2010-09-07. Retrieved 2011-03-19.
- ↑ "GNU Octave Manual. Appendix G Installing Octave" . Retrieved 2011-03-19.
- ↑ "Reference for Armadillo 1.1.8. Examples of Matlab/Octave syntax and conceptually corresponding Armadillo syntax" . Retrieved 2011-03-19.
- ↑ "Blitz++ User's Guide. 3. Array Expressions". Archived from the original on 2011-03-23. Retrieved 2011-03-19.