
A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

In physics, the Coriolis force is an inertial force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
The vorticity equation of fluid dynamics describes the evolution of the vorticity ω of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:
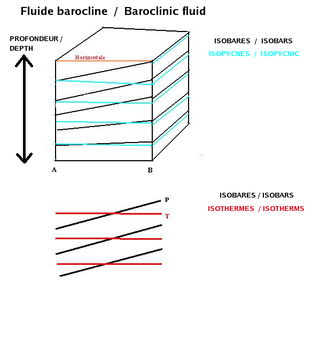
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure. A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks
In atmospheric science, geostrophic flow is the theoretical wind that would result from an exact balance between the Coriolis force and the pressure gradient force. This condition is called geostrophic equilibrium or geostrophic balance. The geostrophic wind is directed parallel to isobars. This balance seldom holds exactly in nature. The true wind almost always differs from the geostrophic wind due to other forces such as friction from the ground. Thus, the actual wind would equal the geostrophic wind only if there were no friction and the isobars were perfectly straight. Despite this, much of the atmosphere outside the tropics is close to geostrophic flow much of the time and it is a valuable first approximation. Geostrophic flow in air or water is a zero-frequency inertial wave.
In fluid mechanics, the Taylor–Proudman theorem states that when a solid body is moved slowly within a fluid that is steadily rotated with a high angular velocity , the fluid velocity will be uniform along any line parallel to the axis of rotation. must be large compared to the movement of the solid body in order to make the Coriolis force large compared to the acceleration terms.
The Coriolis frequencyƒ, also called the Coriolis parameter or Coriolis coefficient, is equal to twice the rotation rate Ω of the Earth multiplied by the sine of the latitude .
The Sverdrup balance, or Sverdrup relation, is a theoretical relationship between the wind stress exerted on the surface of the open ocean and the vertically integrated meridional (north-south) transport of ocean water.
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis, especially along the polar front, and in analyzing flow in the ocean.
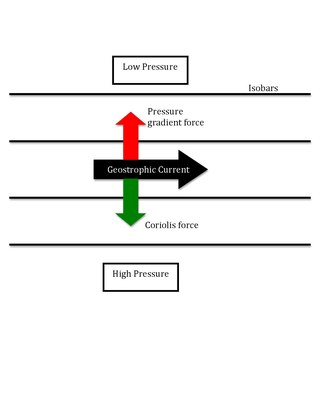
A geostrophic current is an oceanic current in which the pressure gradient force is balanced by the Coriolis effect. The direction of geostrophic flow is parallel to the isobars, with the high pressure to the right of the flow in the Northern Hemisphere, and the high pressure to the left in the Southern Hemisphere. This concept is familiar from weather maps, whose isobars show the direction of geostrophic winds. Geostrophic flow may be either barotropic or baroclinic. A geostrophic current may also be thought of as a rotating shallow water wave with a frequency of zero.
In fluid mechanics, Kelvin's circulation theorem states:
In a barotropic, ideal fluid with conservative body forces, the circulation around a closed curve moving with the fluid remains constant with time.

Inertial waves, also known as inertial oscillations, are a type of mechanical wave possible in rotating fluids. Unlike surface gravity waves commonly seen at the beach or in the bathtub, inertial waves flow through the interior of the fluid, not at the surface. Like any other kind of wave, an inertial wave is caused by a restoring force and characterized by its wavelength and frequency. Because the restoring force for inertial waves is the Coriolis force, their wavelengths and frequencies are related in a peculiar way. Inertial waves are transverse. Most commonly they are observed in atmospheres, oceans, lakes, and laboratory experiments. Rossby waves, geostrophic currents, and geostrophic winds are examples of inertial waves. Inertial waves are also likely to exist in the molten core of the rotating Earth.
The derivation of the Navier–Stokes equations as well as their application and formulation for different families of fluids, is an important exercise in fluid dynamics with applications in mechanical engineering, physics, chemistry, heat transfer, and electrical engineering. A proof explaining the properties and bounds of the equations, such as Navier–Stokes existence and smoothness, is one of the important unsolved problems in mathematics.
In atmospheric science, balanced flow is an idealisation of atmospheric motion. The idealisation consists in considering the behaviour of one isolated parcel of air having constant density, its motion on a horizontal plane subject to selected forces acting on it and, finally, steady-state conditions.
In fluid dynamics, the Coriolis–Stokes force is a forcing of the mean flow in a rotating fluid due to interaction of the Coriolis effect and wave-induced Stokes drift. This force acts on water independently of the wind stress.
Q-vectors are used in atmospheric dynamics to understand physical processes such as vertical motion and frontogenesis. Q-vectors are not physical quantities that can be measured in the atmosphere but are derived from the quasi-geostrophic equations and can be used in the previous diagnostic situations. On meteorological charts, Q-vectors point toward upward motion and away from downward motion. Q-vectors are an alternative to the omega equation for diagnosing vertical motion in the quasi-geostrophic equations.
In fluid dynamics, the Craik–Leibovich (CL) vortex force describes a forcing of the mean flow through wave–current interaction, specifically between the Stokes drift velocity and the mean-flow vorticity. The CL vortex force is used to explain the generation of Langmuir circulations by an instability mechanism. The CL vortex-force mechanism was derived and studied by Sidney Leibovich and Alex D. D. Craik in the 1970s and 80s, in their studies of Langmuir circulations.
In fluid dynamics, Hicks equation, sometimes also referred as Bragg–Hawthorne equation or Squire–Long equation, is a partial differential equation that describes the distribution of stream function for axisymmetric inviscid fluid, named after William Mitchinson Hicks, who derived it first in 1898. The equation was also re-derived by Stephen Bragg and William Hawthorne in 1950 and by Robert R. Long in 1953 and by Herbert Squire in 1956. The Hicks equation without swirl was first introduced by George Gabriel Stokes in 1842. The Grad–Shafranov equation appearing in plasma physics also takes the same form as the Hicks equation.































