
A scanning tunneling microscope (STM) is a type of microscope used for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer, then at IBM Zürich, the Nobel Prize in Physics in 1986. STM senses the surface by using an extremely sharp conducting tip that can distinguish features smaller than 0.1 nm with a 0.01 nm depth resolution. This means that individual atoms can routinely be imaged and manipulated. Most microscopes are built for use in ultra-high vacuum at temperatures approaching zero kelvin, but variants exist for studies in air, water and other environments, and for temperatures over 1000 °C.
The Gram–Charlier A series, and the Edgeworth series are series that approximate a probability distribution in terms of its cumulants. The series are the same; but, the arrangement of terms differ. The key idea of these expansions is to write the characteristic function of the distribution whose probability density function f is to be approximated in terms of the characteristic function of a distribution with known and suitable properties, and to recover f through the inverse Fourier transform.
A heterojunction is an interface between two layers or regions of dissimilar semiconductors. These semiconducting materials have unequal band gaps as opposed to a homojunction. It is often advantageous to engineer the electronic energy bands in many solid-state device applications, including semiconductor lasers, solar cells and transistors. The combination of multiple heterojunctions together in a device is called a heterostructure, although the two terms are commonly used interchangeably. The requirement that each material be a semiconductor with unequal band gaps is somewhat loose, especially on small length scales, where electronic properties depend on spatial properties. A more modern definition of heterojunction is the interface between any two solid-state materials, including crystalline and amorphous structures of metallic, insulating, fast ion conductor and semiconducting materials.
The DLVO theory explains the aggregation of aqueous dispersions quantitatively and describes the force between charged surfaces interacting through a liquid medium. It combines the effects of the van der Waals attraction and the electrostatic repulsion due to the so-called double layer of counterions. The electrostatic part of the DLVO interaction is computed in the mean field approximation in the limit of low surface potentials - that is when the potential energy of an elementary charge on the surface is much smaller than the thermal energy scale, . For two spheres of radius each having a charge separated by a center-to-center distance in a fluid of dielectric constant containing a concentration of monovalent ions, the electrostatic potential takes the form of a screened-Coulomb or Yukawa potential,

In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.

The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.
In quantum mechanics, the Hellmann–Feynman theorem relates the derivative of the total energy with respect to a parameter, to the expectation value of the derivative of the Hamiltonian with respect to that same parameter. According to the theorem, once the spatial distribution of the electrons has been determined by solving the Schrödinger equation, all the forces in the system can be calculated using classical electrostatics.

The chemists Peter Debye and Erich Hückel noticed that solutions that contain ionic solutes do not behave ideally even at very low concentrations. So, while the concentration of the solutes is fundamental to the calculation of the dynamics of a solution, they theorized that an extra factor that they termed gamma is necessary to the calculation of the activity coefficients of the solution. Hence they developed the Debye–Hückel equation and Debye–Hückel limiting law. The activity is only proportional to the concentration and is altered by a factor known as the activity coefficient . This factor takes into account the interaction energy of ions in solution.
Surface states are electronic states found at the surface of materials. They are formed due to the sharp transition from solid material that ends with a surface and are found only at the atom layers closest to the surface. The termination of a material with a surface leads to a change of the electronic band structure from the bulk material to the vacuum. In the weakened potential at the surface, new electronic states can be formed, so called surface states.
The Poisson–Boltzmann equation is a useful equation in many settings, whether it be to understand physiological interfaces, polymer science, electron interactions in a semiconductor, or more. It aims to describe the distribution of the electric potential in solution in the direction normal to a charged surface. This distribution is important to determine how the electrostatic interactions will affect the molecules in solution. The Poisson–Boltzmann equation is derived via mean-field assumptions. From the Poisson–Boltzmann equation many other equations have been derived with a number of different assumptions.
The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes and plasmas. It is a linearized Poisson–Boltzmann model, which assumes an extremely simplified model of electrolyte solution but nevertheless gave accurate predictions of mean activity coefficients for ions in dilute solution. The Debye–Hückel equation provides a starting point for modern treatments of non-ideality of electrolyte solutions.
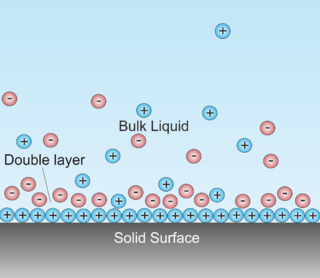
A double layer is a structure that appears on the surface of an object when it is exposed to a fluid. The object might be a solid particle, a gas bubble, a liquid droplet, or a porous body. The DL refers to two parallel layers of charge surrounding the object. The first layer, the surface charge, consists of ions adsorbed onto the object due to chemical interactions. The second layer is composed of ions attracted to the surface charge via the Coulomb force, electrically screening the first layer. This second layer is loosely associated with the object. It is made of free ions that move in the fluid under the influence of electric attraction and thermal motion rather than being firmly anchored. It is thus called the "diffuse layer". (-> this description of DL is not right, at least concerning the electrode/electrolyte interface. Here DL refers to charge separation at the interface with the electrode possessing negative charge and the electrolyte positive charge. The two layers are separated by some molecular distance. The two layers mentioned in above description are all at the electrolyte side.

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
This article relates the Schrödinger equation with the path integral formulation of quantum mechanics using a simple nonrelativistic one-dimensional single-particle Hamiltonian composed of kinetic and potential energy.
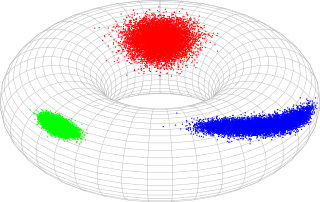
In probability theory and statistics, the bivariate von Mises distribution is a probability distribution describing values on a torus. It may be thought of as an analogue on the torus of the bivariate normal distribution. The distribution belongs to the field of directional statistics. The general bivariate von Mises distribution was first proposed by Kanti Mardia in 1975. One of its variants is today used in the field of bioinformatics to formulate a probabilistic model of protein structure in atomic detail, such as backbone-dependent rotamer libraries.
Adsorption of polyelectrolytes on solid substrates is a surface phenomenon where long-chained polymer molecules with charged groups bind to a surface that is charged in the opposite polarity. On the molecular level, the polymers do not actually bond to the surface, but tend to "stick" to the surface via intermolecular forces and the charges created by the dissociation of various side groups of the polymer. Because the polymer molecules are so long, they have a large amount of surface area with which to contact the surface and thus do not desorb as small molecules are likely to do. This means that adsorbed layers of polyelectrolytes form a very durable coating. Due to this important characteristic of polyelectrolyte layers they are used extensively in industry as flocculants, for solubilization, as supersorbers, antistatic agents, as oil recovery aids, as gelling aids in nutrition, additives in concrete, or for blood compatibility enhancement to name a few.

Double layer forces occur between charged objects across liquids, typically water. This force acts over distances that are comparable to the Debye length, which is on the order of one to a few tenths of nanometers. The strength of these forces increases with the magnitude of the surface charge density. For two similarly charged objects, this force is repulsive and decays exponentially at larger distances, see figure. For unequally charged objects and eventually at shorted distances, these forces may also be attractive. The theory due to Derjaguin, Landau, Verwey, and Overbeek (DLVO) combines such double layer forces together with Van der Waals forces in order to estimate the actual interaction potential between colloidal particles.

The theory of causal fermion systems is an approach to describe fundamental physics. It provides a unification of the weak, the strong and the electromagnetic forces with gravity at the level of classical field theory. Moreover, it gives quantum mechanics as a limiting case and has revealed close connections to quantum field theory. Therefore, it is a candidate for a unified physical theory. Instead of introducing physical objects on a preexisting spacetime manifold, the general concept is to derive spacetime as well as all the objects therein as secondary objects from the structures of an underlying causal fermion system. This concept also makes it possible to generalize notions of differential geometry to the non-smooth setting. In particular, one can describe situations when spacetime no longer has a manifold structure on the microscopic scale. As a result, the theory of causal fermion systems is a proposal for quantum geometry and an approach to quantum gravity.
Exponential Tilting (ET), Exponential Twisting, or Exponential Change of Measure (ECM) is a distribution shifting technique used in many parts of mathematics. The different exponential tiltings of a random variable is known as the natural exponential family of .

A phonovoltaic (pV) cell converts vibrational (phonons) energy into a direct current much like the photovoltaic effect in a photovoltaic (PV) cell converts light (photon) into power. That is, it uses a p-n junction to separate the electrons and holes generated as valence electrons absorb optical phonons more energetic than the band gap, and then collects them in the metallic contacts for use in a circuit. The pV cell is an application of heat transfer physics and competes with other thermal energy harvesting devices like the thermoelectric generator.












