This was the dial that Hugo Michnik invented and studied. By simplifying the general example so:
The proof
The first wire  is orientated north-south at a constant distance
is orientated north-south at a constant distance  from the dial plate
from the dial plate 
The second wire  is orientated east-west at a constant distance
is orientated east-west at a constant distance  from the dial plate
from the dial plate  (thus
(thus  is orthogonal to
is orthogonal to  which lies on the plane of the meridian ).
which lies on the plane of the meridian ).
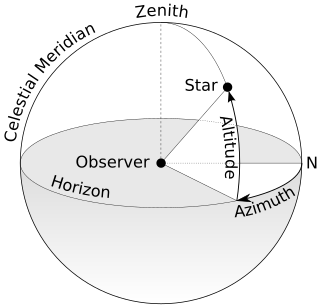
In this proof  (pronounced phi) is the latitude of the dial plate.
(pronounced phi) is the latitude of the dial plate.
Respectively,  and
and  are the vertical projections of wires
are the vertical projections of wires  and
and  on the dial plate
on the dial plate  .
.
Point  is the point on the dial plate directly under the two wires' intersection.
is the point on the dial plate directly under the two wires' intersection.
That point is the origin of the X,Y co-ordinate system referred to below.
The X-axis is the east–west line passing through the origin. The Y-axis is the north–south line passing through the origin. The positive Y direction is northward.
One can show that if the position of the sun is known and determined by the spherical coordinates  et
et  (pronounced t-dot and delta, respectively the known as the hour angle et declination), the co-ordinates
(pronounced t-dot and delta, respectively the known as the hour angle et declination), the co-ordinates  and
and  of point
of point  , the intersection on the two shadows on the dial-plate
, the intersection on the two shadows on the dial-plate  have values of :
have values of :

Eliminating the variable  in the two preceding equations, one obtains a new equation defined for
in the two preceding equations, one obtains a new equation defined for  and
and  which gives, as a function of the latitude
which gives, as a function of the latitude  and the solar hour angle solaire
and the solar hour angle solaire  , the equation of the trace of the sun associated with the local apparent time. In its simplest form this equation is written:
, the equation of the trace of the sun associated with the local apparent time. In its simplest form this equation is written:

This relation shows that the hour traces are indeed line segments and the meeting-point of these line segments is the point  :
:


In other words, point C is south of point O (where the wires intersect), by a distance of 
 is the latitude.
is the latitude.
- Special case
If one arranges the two wire heights  and
and  such :
such :

then the equation for the hour lines can be simply written as:

at all times, the intersection  of the shadows on the dial plate
of the shadows on the dial plate  is such that the angle
is such that the angle  is equal to the hour angle
is equal to the hour angle  of the sun so thus represents solar time.
of the sun so thus represents solar time.
So provided the sundial respects the la condition  the trace of the sun corresponds to the hour-angle shown by lines (rays) centred on the point
the trace of the sun corresponds to the hour-angle shown by lines (rays) centred on the point  and the 13 rays that correspond to the hours 6:00, 7:00, 8:00, 9:00... 15:00, 16:00, 17:00, 18:00 are regularly spaced at a constant angle of 15°, about point C. [lower-alpha 1]
and the 13 rays that correspond to the hours 6:00, 7:00, 8:00, 9:00... 15:00, 16:00, 17:00, 18:00 are regularly spaced at a constant angle of 15°, about point C. [lower-alpha 1]