In the mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points.

In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points.

In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric tensor on M consists of a metric tensor at each point p of M that varies smoothly with p.

In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. In modern mathematical notation, the role is sometimes swapped.
In numerical analysis, polynomial interpolation is the interpolation of a given bivariate data set by the polynomial of lowest possible degree that passes through the points of the dataset.
In the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is an interpolation polynomial for a given set of data points. The Newton polynomial is sometimes called Newton's divided differences interpolation polynomial because the coefficients of the polynomial are calculated using Newton's divided differences method.

In numerical analysis, the Lagrange interpolating polynomial is the unique polynomial of lowest degree that interpolates a given set of data.

In physics, Hooke's law is an empirical law which states that the force needed to extend or compress a spring by some distance scales linearly with respect to that distance—that is, Fs = kx, where k is a constant factor characteristic of the spring, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis. Hooke states in the 1678 work that he was aware of the law since 1660.
In the mathematical field of numerical analysis, spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline. That is, instead of fitting a single, high-degree polynomial to all of the values at once, spline interpolation fits low-degree polynomials to small subsets of the values, for example, fitting nine cubic polynomials between each of the pairs of ten points, instead of fitting a single degree-ten polynomial to all of them. Spline interpolation is often preferred over polynomial interpolation because the interpolation error can be made small even when using low-degree polynomials for the spline. Spline interpolation also avoids the problem of Runge's phenomenon, in which oscillation can occur between points when interpolating using high-degree polynomials.
In numerical analysis, a cubic Hermite spline or cubic Hermite interpolator is a spline where each piece is a third-degree polynomial specified in Hermite form, that is, by its values and first derivatives at the end points of the corresponding domain interval.
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. It is used to solve systems of linear differential equations. In the theory of Lie groups, the matrix exponential gives the exponential map between a matrix Lie algebra and the corresponding Lie group.
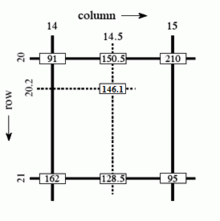
Trilinear interpolation is a method of multivariate interpolation on a 3-dimensional regular grid. It approximates the value of a function at an intermediate point within the local axial rectangular prism linearly, using function data on the lattice points. For an arbitrary, unstructured mesh, other methods of interpolation must be used; if all the mesh elements are tetrahedra, then barycentric coordinates provide a straightforward procedure.
In mathematics, trigonometric interpolation is interpolation with trigonometric polynomials. Interpolation is the process of finding a function which goes through some given data points. For trigonometric interpolation, this function has to be a trigonometric polynomial, that is, a sum of sines and cosines of given periods. This form is especially suited for interpolation of periodic functions.

In mathematics, bicubic interpolation is an extension of cubic spline interpolation for interpolating data points on a two-dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation. Bicubic interpolation can be accomplished using either Lagrange polynomials, cubic splines, or cubic convolution algorithm.
This article derives the main properties of rotations in 3-dimensional space.

In physics and continuum mechanics, deformation is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.
In algebra, a multilinear polynomial is a multivariate polynomial that is linear in each of its variables separately, but not necessarily simultaneously. It is a polynomial in which no variable occurs to a power of 2 or higher; that is, each monomial is a constant times a product of distinct variables. For example f(x,y,z) = 3xy + 2.5 y - 7z is a multilinear polynomial of degree 2 whereas f(x,y,z) = x² +4y is not. The degree of a multilinear polynomial is the maximum number of distinct variables occurring in any monomial.
Radial basis function (RBF) interpolation is an advanced method in approximation theory for constructing high-order accurate interpolants of unstructured data, possibly in high-dimensional spaces. The interpolant takes the form of a weighted sum of radial basis functions, like for example Gaussian distributions. RBF interpolation is a mesh-free method, meaning the nodes need not lie on a structured grid, and does not require the formation of a mesh. It is often spectrally accurate and stable for large numbers of nodes even in high dimensions.