The Grashof number (Gr) is a dimensionless number in fluid dynamics and heat transfer which approximates the ratio of the buoyancy to viscous force acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number. It's believed to be named after Franz Grashof. Though this grouping of terms had already been in use, it wasn't named until around 1921, 28 years after Franz Grashof's death. It's not very clear why the grouping was named after him.

Physical geodesy is the study of the physical properties of Earth's gravity and its potential field, with a view to their application in geodesy.
Isostasy or isostatic equilibrium is the state of gravitational equilibrium between Earth's crust and mantle such that the crust "floats" at an elevation that depends on its thickness and density. This concept is invoked to explain how different topographic heights can exist at Earth's surface. Although originally defined in terms of continental crust and mantle, it has subsequently been interpreted in terms of lithosphere and asthenosphere, particularly with respect to oceanic island volcanoes, such as the Hawaiian Islands.

Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson.

In the general theory of relativity, the Einstein field equations relate the geometry of spacetime to the distribution of matter within it.
In geophysics, the free-air gravity anomaly, often simply called the free-air anomaly, is the measured gravity anomaly after a free-air correction is applied to account for the elevation at which a measurement is made. It does so by adjusting these measurements of gravity to what would have been measured at a reference level, which is commonly taken as mean sea level or the geoid.
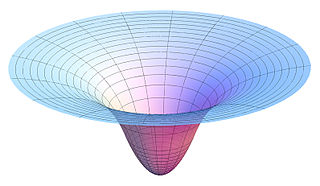
In classical mechanics, the gravitational potential at a location is equal to the work per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.
The gravity anomaly at a location on the Earth's surface is the difference between the observed value of gravity and the value predicted by a theoretical model. If the Earth was an ideal oblate spheroid of uniform density, then the gravity measured at every point on its surface would be given precisely by a simple formula. However, the Earth has a rugged surface and nonuniform composition, which distorts its gravitational field. The theoretical value of gravity can be corrected for altitude and the effects of nearby terrain, but it usually still differs slightly from the measured value. This gravity anomaly can reveal the presence of subsurface structures of unusual density. For example, a mass of dense ore below the surface will give a positive anomaly due to the increased gravitational attraction of the ore.

Gravimetry is the measurement of the strength of a gravitational field. Gravimetry may be used when either the magnitude of a gravitational field or the properties of matter responsible for its creation are of interest.
A classical field theory is a physical theory that predicts how one or more physical fields interact with matter through field equations, without considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field theory' is specifically meant to describe electromagnetism and gravitation, two of the fundamental forces of nature.

The Kerr–Newman metric is the most general asymptotically flat, stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions, that is, of solutions to the Einstein–Maxwell equations which account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.

The surface gravity, g, of an astronomical object is the gravitational acceleration experienced at its surface at the equator, including the effects of rotation. The surface gravity may be thought of as the acceleration due to gravity experienced by a hypothetical test particle which is very close to the object's surface and which, in order not to disturb the system, has negligible mass. For objects where the surface is deep in the atmosphere and the radius not known, the surface gravity is given at the 1 bar pressure level in the atmosphere.

In physics, precisely in the study of the theory of general relativity and many alternatives to it, the post-Newtonian formalism is a calculational tool that expresses Einstein's (nonlinear) equations of gravity in terms of the lowest-order deviations from Newton's law of universal gravitation. This allows approximations to Einstein's equations to be made in the case of weak fields. Higher-order terms can be added to increase accuracy, but for strong fields, it may be preferable to solve the complete equations numerically. Some of these post-Newtonian approximations are expansions in a small parameter, which is the ratio of the velocity of the matter forming the gravitational field to the speed of light, which in this case is better called the speed of gravity. In the limit, when the fundamental speed of gravity becomes infinite, the post-Newtonian expansion reduces to Newton's law of gravity.

The gravity of Earth, denoted by g, is the net acceleration that is imparted to objects due to the combined effect of gravitation and the centrifugal force . It is a vector (physics) quantity, whose direction coincides with a plumb bob and strength or magnitude is given by the norm .

The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
In physics, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics that is equivalent to Newton's law of universal gravitation. It is named after Carl Friedrich Gauss. It states that the flux of the gravitational field over any closed surface is equal to the mass enclosed. Gauss's law for gravity is often more convenient to work from than is Newton's law.
Newton–Cartan theory is a geometrical re-formulation, as well as a generalization, of Newtonian gravity first introduced by Élie Cartan and Kurt Friedrichs and later developed by Dautcourt, Dixon, Dombrowski and Horneffer, Ehlers, Havas, Künzle, Lottermoser, Trautman, and others. In this re-formulation, the structural similarities between Newton's theory and Albert Einstein's general theory of relativity are readily seen, and it has been used by Cartan and Friedrichs to give a rigorous formulation of the way in which Newtonian gravity can be seen as a specific limit of general relativity, and by Jürgen Ehlers to extend this correspondence to specific solutions of general relativity.
f(R) is a type of modified gravity theory which generalizes Einstein's general relativity. f(R) gravity is actually a family of theories, each one defined by a different function, f, of the Ricci scalar, R. The simplest case is just the function being equal to the scalar; this is general relativity. As a consequence of introducing an arbitrary function, there may be freedom to explain the accelerated expansion and structure formation of the Universe without adding unknown forms of dark energy or dark matter. Some functional forms may be inspired by corrections arising from a quantum theory of gravity. f(R) gravity was first proposed in 1970 by Hans Adolph Buchdahl. It has become an active field of research following work by Starobinsky on cosmic inflation. A wide range of phenomena can be produced from this theory by adopting different functions; however, many functional forms can now be ruled out on observational grounds, or because of pathological theoretical problems.
In astrophysics, the virial mass is the mass of a gravitationally bound astrophysical system, assuming the virial theorem applies. In the context of galaxy formation and dark matter halos, the virial mass is defined as the mass enclosed within the virial radius of a gravitationally bound system, a radius within which the system obeys the virial theorem. The virial radius is determined using a "top-hat" model. A spherical "top hat" density perturbation destined to become a galaxy begins to expand, but the expansion is halted and reversed due to the mass collapsing under gravity until the sphere reaches equilibrium – it is said to be virialized. Within this radius, the sphere obeys the virial theorem which says that the average kinetic energy is equal to minus one half times the average potential energy, , and this radius defines the virial radius.
The gravity of Mars is a natural phenomenon, due to the law of gravity, or gravitation, by which all things with mass around the planet Mars are brought towards it. It is weaker than Earth's gravity due to the planet's smaller mass. The average gravitational acceleration on Mars is 3.72076 ms−2 and it varies. In general, topography-controlled isostasy drives the short wavelength free-air gravity anomalies. At the same time, convective flow and finite strength of the mantle lead to long-wavelength planetary-scale free-air gravity anomalies over the entire planet. Variation in crustal thickness, magmatic and volcanic activities, impact-induced Moho-uplift, seasonal variation of polar ice caps, atmospheric mass variation and variation of porosity of the crust could also correlate to the lateral variations. Over the years models consisting of an increasing but limited number of spherical harmonics have been produced. Maps produced have included free-air gravity anomaly, Bouguer gravity anomaly, and crustal thickness. In some areas of Mars there is a correlation between gravity anomalies and topography. Given the known topography, higher resolution gravity field can be inferred. Tidal deformation of Mars by the Sun or Phobos can be measured by its gravity. This reveals how stiff the interior is, and shows that the core is partially liquid. The study of surface gravity of Mars can therefore yield information about different features and provide beneficial information for future landings.





















