Bound entanglement

Last updated

Bound entanglement is a weak form of quantum entanglement, from which no singlets can be distilled with local operations and classical communication (LOCC).

Bound entanglement was discovered by M. Horodecki, P. Horodecki, and R. Horodecki. Bipartite entangled states that have a non-negative partial transpose are all bound-entangled. Moreover, a particular quantum state for 2x4 systems has been presented. [1] Such states are not detected by the Peres-Horodecki criterion as entangled, thus other entanglement criteria are needed for their detection. There are a number of examples for such states. [2] [3] [4] [5]

There are also multipartite entangled states that have a negative partial transpose with respect to some bipartitions, while they have a positive partial transpose to the other partitions, nevertheless, they are undistillable. [6]

The possible existence of bipartite bound entangled states with a negative partial transpose is still under intensive study. [7]

Properties of bound entangled states with a positive partial transpose

Bipartite bound entangled states do not exist in 2x2 or 2x3 systems, only in larger ones.

Rank-2 bound entangled states do not exist. [8]

Bipartite bound entangled states with a positive partial transpose are useless for teleportation, as they cannot lead to a larger fidelity than the classical limit. [9]

Bound entangled states with a positive partial transpose in 3x3 systems have a Schmidt number 2. [10]

It has been shown that bipartite bound entangled states with a positive partial transpose exist in symmetric systems. It has also been shown that in symmetric systems multipartite bound entangled states exists for which all partial transposes are non-negative. [11] [12]

Asher Peres conjectured that bipartite bound entangled states with positive partial transpose cannot violate a Bell inequality. [13] After a long search for counterexamples, the conjecture turned out to be false. [14]

While no singlets can be distilled from bound entangled state, they can be still useful for some quantum information processing applications. Bound entanglement can be activated. [15] Any entangled state can enhance the teleportation power of some other state. This holds even if the state is bound entangled. [16] Bipartite entangled states with a non-negative partial transpose can be more useful for quantum metrology than separable states. [17] Families of bound entangled states known analytically even for high dimension that outperform separable states for metrology. For large dimensions they approach asymptotically the maximal precision achievable by bipartite quantum states. [18] There are bipartite bound entangled states that are not more useful than separable states, but if an ancilla is added to one of the subsystems then they outperform separable states in metrology. [19]

Related Research Articles

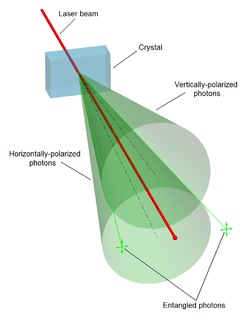
Quantum entanglement Correlation between measurements of quantum subsystems, even when spatially separated

Quantum entanglement is a physical phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics lacking in classical mechanics.

The Peres–Horodecki criterion is a necessary condition, for the joint density matrix of two quantum mechanical systems and , to be separable. It is also called the PPT criterion, for positive partial transpose. In the 2x2 and 2x3 dimensional cases the condition is also sufficient. It is used to decide the separability of mixed states, where the Schmidt decomposition does not apply. The theorem was discovered in 1996 by Asher Peres and the Horodecki family

In quantum mechanics, separable states are quantum states belonging to a composite space that can be factored into individual states belonging to separate subspaces. A state is said to be entangled if it is not separable. In general, determining if a state is separable is not straightforward and the problem is classed as NP-hard.

Topological order Type of order at absolute zero

In physics, topological order is a kind of order in the zero-temperature phase of matter. Macroscopically, topological order is defined and described by robust ground state degeneracy and quantized non-Abelian geometric phases of degenerate ground states. Microscopically, topological orders correspond to patterns of long-range quantum entanglement. States with different topological orders cannot change into each other without a phase transition.

In physics, the no-broadcasting theorem is a result of quantum information theory. In the case of pure quantum states, it is a corollary of the no-cloning theorem. The no-cloning theorem for pure states says that it is impossible to create two copies of an unknown state given a single copy of the state. Since quantum states cannot be copied in general, they cannot be broadcast. Here, the word "broadcast" is used in the sense of conveying the state to two or more recipients. For multiple recipients to each receive the state, there must be, in some sense, a way of duplicating the state. The no-broadcast theorem generalizes the no-cloning theorem for mixed states.

A NOON state is a quantum-mechanical many-body entangled state:

In quantum information theory, the reduction criterion is a necessary condition a mixed state must satisfy in order for it to be separable. In other words, the reduction criterion is a separability criterion. It was first proved and independently formulated in 1999. Violation of the reduction criterion is closely related to the distillability of the state in question.

In theoretical physics, quantum nonlocality refers to the phenomenon by which the measurement statistics of a multipartite quantum system do not admit an interpretation in terms of a local realistic theory. Quantum nonlocality has been experimentally verified under different physical assumptions. Any physical theory that aims at superseding or replacing quantum theory should account for such experiments and therefore cannot fulfill local realism; quantum nonlocality is a property of the universe that is independent of our description of nature.

The one-way or measurement-based quantum computer (MBQC) is a method of quantum computing that first prepares an entangled resource state, usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements.

In quantum information and quantum computing, a cluster state is a type of highly entangled state of multiple qubits. Cluster states are generated in lattices of qubits with Ising type interactions. A cluster C is a connected subset of a d-dimensional lattice, and a cluster state is a pure state of the qubits located on C. They are different from other types of entangled states such as GHZ states or W states in that it is more difficult to eliminate quantum entanglement in the case of cluster states. Another way of thinking of cluster states is as a particular instance of graph states, where the underlying graph is a connected subset of a d-dimensional lattice. Cluster states are especially useful in the context of the one-way quantum computer. For a comprehensible introduction to the topic see.

A quantum sensor is a device that works by detecting variations in microgravity using the principles of quantum physics, which is based on manipulating nature at the sub-molecular level. Quantum sensing utilizes properties of quantum mechanics, such as quantum entanglement, quantum interference, and quantum state squeezing, which have optimized precision and beat current limits in sensor technology and evade the Heisenberg uncertainty principle. The field of quantum sensing deals with the design and engineering of quantum sources and quantum measurements that are able to beat the performance of any classical strategy in a number of technological applications. This can be done with photonic systems or solid state systems.

In the case of systems composed of subsystems, the classification of quantum-entangledstates is richer than in the bipartite case. Indeed, in multipartite entanglement apart from fully separable states and fully entangled states, there also exists the notion of partially separable states.

Frank Verstraete Belgian quantum physicist

Frank Verstraete is a Belgian quantum physicist who is working on the interface between quantum information theory and quantum many-body physics. He pioneered the use of tensor networks and entanglement theory in quantum many body systems. He is full professor at the Faculty of Physics at Ghent University.

In quantum information theory, quantum discord is a measure of nonclassical correlations between two subsystems of a quantum system. It includes correlations that are due to quantum physical effects but do not necessarily involve quantum entanglement.

In quantum mechanics, negativity is a measure of quantum entanglement which is easy to compute. It is a measure deriving from the PPT criterion for separability. It has shown to be an entanglement monotone and hence a proper measure of entanglement.

In quantum information theory, a quantum catalyst is an entanglement-assisted local quantum operations and classical communication, a special ancillary quantum state whose presence enables certain local transformations that would otherwise be impossible. Quantum catalytic behaviour has been shown to arise from the phenomenon of catalytic majorization.

Sandu Popescu British physicist

Sandu Popescu is a Romanian-British physicist working in the foundations of quantum mechanics and quantum information.

Continuous-variable (CV) quantum information is the area of quantum information science that makes use of physical observables, like the strength of an electromagnetic field, whose numerical values belong to continuous intervals. One primary application is quantum computing. In a sense, continuous-variable quantum computation is "analog", while quantum computation using qubits is "digital." In more technical terms, the former makes use of Hilbert spaces that are infinite-dimensional, while the Hilbert spaces for systems comprising collections of qubits are finite-dimensional. One motivation for studying continuous-variable quantum computation is to understand what resources are necessary to make quantum computers more powerful than classical ones.

Spin squeezing is a quantum process that decreases the variance of one of the angular momentum components in an ensemble of particles with a spin. The quantum states obtained are called spin squeezed states. Such states can be used for quantum metrology, as they can provide a better precision for estimating a rotation angle than classical interferometers.

In quantum physics, monogamy describes the fundamental principle that quantum entanglement cannot be freely shared between arbitrarily many parties.

References

  1. ↑ Horodecki, Michał; Horodecki, Paweł; Horodecki, Ryszard (15 June 1998). "Mixed-State Entanglement and Distillation: Is there a "Bound" Entanglement in Nature?". Physical Review Letters. 80 (24): 5239–5242. arXiv: quant-ph/9801069 . Bibcode:1998PhRvL..80.5239H. doi:10.1103/PhysRevLett.80.5239. S2CID   111379972.
  2. ↑ Bruß, Dagmar; Peres, Asher (4 February 2000). "Construction of quantum states with bound entanglement". Physical Review A. 61 (3): 030301. arXiv: quant-ph/9911056 . Bibcode:2000PhRvA..61c0301B. doi:10.1103/PhysRevA.61.030301. S2CID   7019402.
  3. ↑ Bennett, Charles H.; DiVincenzo, David P.; Mor, Tal; Shor, Peter W.; Smolin, John A.; Terhal, Barbara M. (28 June 1999). "Unextendible Product Bases and Bound Entanglement" (PDF). Physical Review Letters. 82 (26): 5385–5388. arXiv: quant-ph/9808030 . Bibcode:1999PhRvL..82.5385B. doi:10.1103/PhysRevLett.82.5385. S2CID   14688979.
  4. ↑ Breuer, Heinz-Peter (22 August 2006). "Optimal Entanglement Criterion for Mixed Quantum States". Physical Review Letters. 97 (8): 080501. arXiv: quant-ph/0605036 . Bibcode:2006PhRvL..97h0501B. doi:10.1103/PhysRevLett.97.080501. PMID   17026285. S2CID   14406014.
  5. ↑ Piani, Marco; Mora, Caterina E. (4 January 2007). "Class of positive-partial-transpose bound entangled states associated with almost any set of pure entangled states". Physical Review A. 75 (1): 012305. arXiv: quant-ph/0607061 . Bibcode:2007PhRvA..75a2305P. doi:10.1103/PhysRevA.75.012305. S2CID   55900164.
  6. ↑ Smolin, John A. (9 February 2001). "Four-party unlockable bound entangled state". Physical Review A. 63 (3): 032306. arXiv: quant-ph/0001001 . Bibcode:2001PhRvA..63c2306S. doi:10.1103/PhysRevA.63.032306. S2CID   119474939.
  7. ↑ DiVincenzo, David P.; Shor, Peter W.; Smolin, John A.; Terhal, Barbara M.; Thapliyal, Ashish V. (17 May 2000). "Evidence for bound entangled states with negative partial transpose". Physical Review A. 61 (6): 062312. arXiv: quant-ph/9910026 . Bibcode:2000PhRvA..61f2312D. doi:10.1103/PhysRevA.61.062312. S2CID   37213011.
  8. ↑ Horodecki, Pawel; Smolin, John A; Terhal, Barbara M; Thapliyal, Ashish V (January 2003). "Rank two bipartite bound entangled states do not exist". Theoretical Computer Science. 292 (3): 589–596. arXiv: quant-ph/9910122 . doi:10.1016/S0304-3975(01)00376-0. S2CID   43737866.
  9. ↑ Horodecki, Michał; Horodecki, Paweł; Horodecki, Ryszard (1 September 1999). "General teleportation channel, singlet fraction, and quasidistillation". Physical Review A. 60 (3): 1888–1898. arXiv: quant-ph/9807091 . Bibcode:1999PhRvA..60.1888H. doi:10.1103/PhysRevA.60.1888. S2CID   119532807.
  10. ↑ Chen, Lin; Tang, Wai-Shing (2 February 2017). "Schmidt number of bipartite and multipartite states under local projections". Quantum Information Processing. 16 (75): 75. arXiv: 1609.05100 . Bibcode:2017QuIP...16...75C. doi:10.1007/s11128-016-1501-y. S2CID   34893860.
  11. ↑ Tóth, Géza; Gühne, Otfried (1 May 2009). "Entanglement and Permutational Symmetry". Physical Review Letters. 102 (17): 170503. arXiv: 0812.4453 . Bibcode:2009PhRvL.102q0503T. doi:10.1103/PhysRevLett.102.170503. PMID   19518768. S2CID   43527866.
  12. ↑ Tura, J.; Augusiak, R.; Hyllus, P.; Kuś, M.; Samsonowicz, J.; Lewenstein, M. (22 June 2012). "Four-qubit entangled symmetric states with positive partial transpositions". Physical Review A. 85 (6): 060302. arXiv: 1203.3711 . Bibcode:2012PhRvA..85f0302T. doi:10.1103/PhysRevA.85.060302. S2CID   118386611.
  13. ↑ Peres, Asher (1999). "All the Bell Inequalities". Foundations of Physics. 29 (4): 589–614. doi:10.1023/A:1018816310000. S2CID   9697993.
  14. ↑ Vértesi, Tamás; Brunner, Nicolas (December 2014). "Disproving the Peres conjecture by showing Bell nonlocality from bound entanglement". Nature Communications. 5 (1): 5297. arXiv: 1405.4502 . Bibcode:2014NatCo...5.5297V. doi: 10.1038/ncomms6297 . PMID   25370352. S2CID   5135148.
  15. ↑ Horodecki, Paweł; Horodecki, Michał; Horodecki, Ryszard (1 February 1999). "Bound Entanglement Can Be Activated". Physical Review Letters. 82 (5): 1056–1059. arXiv: quant-ph/9806058 . Bibcode:1999PhRvL..82.1056H. doi:10.1103/PhysRevLett.82.1056. S2CID   119390324.
  16. ↑ Masanes, Lluís (17 April 2006). "All Bipartite Entangled States Are Useful for Information Processing". Physical Review Letters. 96 (15): 150501. arXiv: quant-ph/0508071 . Bibcode:2006PhRvL..96o0501M. doi:10.1103/PhysRevLett.96.150501. PMID   16712136. S2CID   10914899.
  17. ↑ Tóth, Géza; Vértesi, Tamás (12 January 2018). "Quantum States with a Positive Partial Transpose are Useful for Metrology". Physical Review Letters. 120 (2): 020506. arXiv: 1709.03995 . Bibcode:2018PhRvL.120b0506T. doi: 10.1103/PhysRevLett.120.020506 . PMID   29376687. S2CID   206306250.
  18. ↑ Pál, Károly F.; Tóth, Géza; Bene, Erika; Vértesi, Tamás (10 May 2021). "Bound entangled singlet-like states for quantum metrology". Physical Review Research. 3 (2): 023101. arXiv: 2002.12409 . Bibcode:2021PhRvR...3b3101P. doi: 10.1103/PhysRevResearch.3.023101 .
  19. ↑ Tóth, Géza; Vértesi, Tamás; Horodecki, Paweł; Horodecki, Ryszard (7 July 2020). "Activating Hidden Metrological Usefulness". Physical Review Letters. 125 (2): 020402. arXiv: 1911.02592 . Bibcode:2020PhRvL.125b0402T. doi: 10.1103/PhysRevLett.125.020402 . PMID   32701319.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.