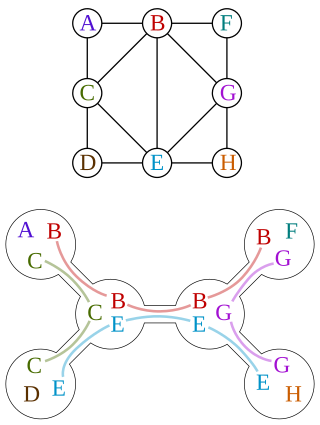
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to define the treewidth of the graph and speed up solving certain computational problems on the graph.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In graph theory, an undirected graph H is called a minor of the graph G if H can be formed from G by deleting edges, vertices and by contracting edges.
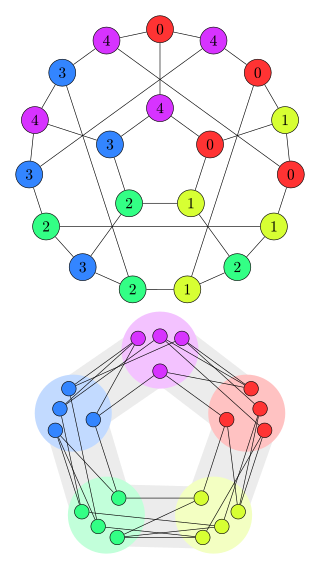
In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.
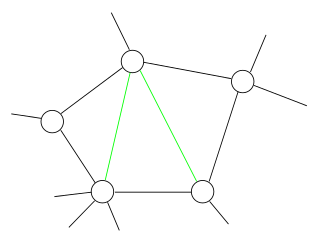
In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs: a chordal completion of a graph is typically called a triangulation of that graph.

Paul D. Seymour is a British mathematician known for his work in discrete mathematics, especially graph theory. He was responsible for important progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture. Many of his recent papers are available from his website.

In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at least one edge out of every cycle in the graph. Removing these edges from the graph breaks all of the cycles, producing an acyclic subgraph of the given graph, often called a directed acyclic graph. A feedback arc set with the fewest possible edges is a minimum feedback arc set and its removal leaves a maximum acyclic subgraph; weighted versions of these optimization problems are also used. If a feedback arc set is minimal, meaning that removing any edge from it produces a subset that is not a feedback arc set, then it has an additional property: reversing all of its edges, rather than removing them, produces a directed acyclic graph.
In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.
In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.
In graph theory, a haven is a certain type of function on sets of vertices in an undirected graph. If a haven exists, it can be used by an evader to win a pursuit–evasion game on the graph, by consulting the function at each step of the game to determine a safe set of vertices to move into. Havens were first introduced by Seymour & Thomas (1993) as a tool for characterizing the treewidth of graphs. Their other applications include proving the existence of small separators on minor-closed families of graphs, and characterizing the ends and clique minors of infinite graphs.

In graph theory, series–parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.

In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :
- Creation of a new vertex v with label i (denoted by i(v))
- Disjoint union of two labeled graphs G and H (denoted by )
- Joining by an edge every vertex labeled i to every vertex labeled j (denoted by η(i,j)), where i ≠ j
- Renaming label i to label j (denoted by ρ(i,j))

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.
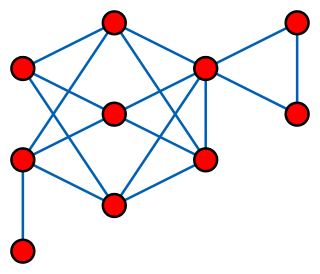
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.
In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and Paul Seymour. Its proof is very long and involved. Kawarabayashi & Mohar (2007) and Lovász (2006) are surveys accessible to nonspecialists, describing the theorem and its consequences.
In graph theory, the tree-depth of a connected undirected graph is a numerical invariant of , the minimum height of a Trémaux tree for a supergraph of . This invariant and its close relatives have gone under many different names in the literature, including vertex ranking number, ordered chromatic number, and minimum elimination tree height; it is also closely related to the cycle rank of directed graphs and the star height of regular languages. Intuitively, where the treewidth of a graph measures how far it is from being a tree, this parameter measures how far a graph is from being a star.
In graph theory, a partial k-tree is a type of graph, defined either as a subgraph of a k-tree or as a graph with treewidth at most k. Many NP-hard combinatorial problems on graphs are solvable in polynomial time when restricted to the partial k-trees, for bounded values of k.
In the study of graph algorithms, Courcelle's theorem is the statement that every graph property definable in the monadic second-order logic of graphs can be decided in linear time on graphs of bounded treewidth. The result was first proved by Bruno Courcelle in 1990 and independently rediscovered by Borie, Parker & Tovey (1992). It is considered the archetype of algorithmic meta-theorems.
In graph theory, a branch of mathematics, Halin's grid theorem states that the infinite graphs with thick ends are exactly the graphs containing subdivisions of the hexagonal tiling of the plane. It was published by Rudolf Halin, and is a precursor to the work of Robertson and Seymour linking treewidth to large grid minors, which became an important component of the algorithmic theory of bidimensionality.
In the mathematical fields of graph theory and finite model theory, the logic of graphs deals with formal specifications of graph properties using sentences of mathematical logic. There are several variations in the types of logical operation that can be used in these sentences. The first-order logic of graphs concerns sentences in which the variables and predicates concern individual vertices and edges of a graph, while monadic second-order graph logic allows quantification over sets of vertices or edges. Logics based on least fixed point operators allow more general predicates over tuples of vertices, but these predicates can only be constructed through fixed-point operators, restricting their power.











