A capital recovery factor is the ratio of a constant annuity to the present value of receiving that annuity for a given length of time. Using an interest rate i, the capital recovery factor is:
where is the number of annuities received. [1]
This is related to the annuity formula, which gives the present value in terms of the annuity, the interest rate, and the number of annuities.
If , the reduces to . Also, as , the .
With an interest rate of i = 10%, and n = 10 years, the CRF = 0.163. This means that a loan of $1,000 at 10% interest will be paid back with 10 annual payments of $163. [2]
Another reading that can be obtained is that the net present value of 10 annual payments of $163 at 10% discount rate is $1,000. [2]
Discounting is a financial mechanism in which a debtor obtains the right to delay payments to a creditor, for a defined period of time, in exchange for a charge or fee. Essentially, the party that owes money in the present purchases the right to delay the payment until some future date. This transaction is based on the fact that most people prefer current interest to delayed interest because of mortality effects, impatience effects, and salience effects. The discount, or charge, is the difference between the original amount owed in the present and the amount that has to be paid in the future to settle the debt.
The net present value (NPV) or net present worth (NPW) applies to a series of cash flows occurring at different times. The present value of a cash flow depends on the interval of time between now and the cash flow. It also depends on the discount rate. NPV accounts for the time value of money. It provides a method for evaluating and comparing capital projects or financial products with cash flows spread over time, as in loans, investments, payouts from insurance contracts plus many other applications.
Internal rate of return (IRR) is a method of calculating an investment’s rate of return. The term internal refers to the fact that the calculation excludes external factors, such as the risk-free rate, inflation, the cost of capital, or financial risk.
In economics and finance, present value (PV), also known as present discounted value, is the value of an expected income stream determined as of the date of valuation. The present value is usually less than the future value because money has interest-earning potential, a characteristic referred to as the time value of money, except during times of zero- or negative interest rates, when the present value will be equal or more than the future value. Time value can be described with the simplified phrase, "A dollar today is worth more than a dollar tomorrow". Here, 'worth more' means that its value is greater than tomorrow. A dollar today is worth more than a dollar tomorrow because the dollar can be invested and earn a day's worth of interest, making the total accumulate to a value more than a dollar by tomorrow. Interest can be compared to rent. Just as rent is paid to a landlord by a tenant without the ownership of the asset being transferred, interest is paid to a lender by a borrower who gains access to the money for a time before paying it back. By letting the borrower have access to the money, the lender has sacrificed the exchange value of this money, and is compensated for it in the form of interest. The initial amount of borrowed funds is less than the total amount of money paid to the lender.
The time value of money is the widely accepted conjecture that there is greater benefit to receiving a sum of money now rather than an identical sum later. It may be seen as an implication of the later-developed concept of time preference.
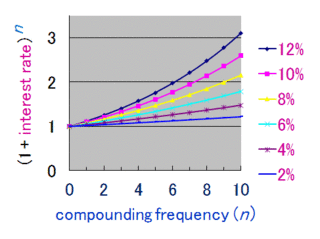
Compound interest is the addition of interest to the principal sum of a loan or deposit, or in other words, interest on principal plus interest. It is the result of reinvesting interest, or adding it to the loaned capital rather than paying it out, or requiring payment from borrower, so that interest in the next period is then earned on the principal sum plus previously accumulated interest. Compound interest is standard in finance and economics.
In finance and economics, the nominal interest rate or nominal rate of interest is either of two distinct things:
Future value is the value of an asset at a specific date. It measures the nominal future sum of money that a given sum of money is "worth" at a specified time in the future assuming a certain interest rate, or more generally, rate of return; it is the present value multiplied by the accumulation function. The value does not include corrections for inflation or other factors that affect the true value of money in the future. This is used in time value of money calculations.
In finance, the duration of a financial asset that consists of fixed cash flows, such as a bond, is the weighted average of the times until those fixed cash flows are received. When the price of an asset is considered as a function of yield, duration also measures the price sensitivity to yield, the rate of change of price with respect to yield, or the percentage change in price for a parallel shift in yields.
Actuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.
The term annual percentage rate of charge (APR), corresponding sometimes to a nominal APR and sometimes to an effective APR (EAPR), is the interest rate for a whole year (annualized), rather than just a monthly fee/rate, as applied on a loan, mortgage loan, credit card, etc. It is a finance charge expressed as an annual rate. Those terms have formal, legal definitions in some countries or legal jurisdictions, but in the United States:
In finance, the equivalent annual cost (EAC) is the cost per year of owning and operating an asset over its entire lifespan. It is calculated by dividing the NPV of a project by the "present value of annuity factor":
In finance, a day count convention determines how interest accrues over time for a variety of investments, including bonds, notes, loans, mortgages, medium-term notes, swaps, and forward rate agreements (FRAs). This determines the number of days between two coupon payments, thus calculating the amount transferred on payment dates and also the accrued interest for dates between payments. The day count is also used to quantify periods of time when discounting a cash-flow to its present value. When a security such as a bond is sold between interest payment dates, the seller is eligible to some fraction of the coupon amount.
In finance, return is a profit on an investment. It comprises any change in value of the investment, and/or cash flows which the investor receives from that investment, such as interest payments, coupons, cash dividends, stock dividends or the payoff from a derivative or structured product. It may be measured either in absolute terms or as a percentage of the amount invested. The latter is also called the holding period return.
The actuarial present value (APV) is the expected value of the present value of a contingent cash flow stream. Actuarial present values are typically calculated for the benefit-payment or series of payments associated with life insurance and life annuities. The probability of a future payment is based on assumptions about the person's future mortality which is typically estimated using a life table.
Mortgage calculators are automated tools that enable users to determine the financial implications of changes in one or more variables in a mortgage financing arrangement. Mortgage calculators are used by consumers to determine monthly repayments, and by mortgage providers to determine the financial suitability of a home loan applicant. Mortgage calculators are frequently on for-profit websites, though the Consumer Financial Protection Bureau has launched its own public mortgage calculator.
In economics, Present value interest factor, also known by the acronym PVIF, is used in finance theory to refer to the output of a calculation, used to determine the monthly payment needed to repay a loan. The calculation has a number of variable factors, which include the quantity borrowed, the given interest rate, the number of regular intervals at which the loan is to be repaid and the term of the loan. For example, if person borrows a lump of money, valued at W, due to be repaid at X intervals per year, at an annual interest rate of Y, for Z years, then the regular payment that will repay this loan can be calculated as follows:
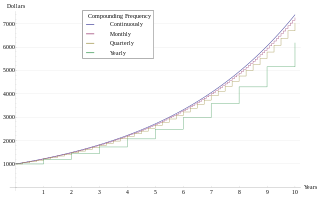
Analogous to continuous compounding, a continuous annuity is an ordinary annuity in which the payment interval is narrowed indefinitely. A (theoretical) continuous repayment mortgage is a mortgage loan paid by means of a continuous annuity.
In investment, an annuity is a series of payments made at equal intervals. Examples of annuities are regular deposits to a savings account, monthly home mortgage payments, monthly insurance payments and pension payments. Annuities can be classified by the frequency of payment dates. The payments (deposits) may be made weekly, monthly, quarterly, yearly, or at any other regular interval of time. Annuities may be calculated by mathematical functions known as "annuity functions".
In finance, a zero coupon swap (ZCS) is an interest rate derivative (IRD). In particular it is a linear IRD, that in its specification is very similar to the much more widely traded interest rate swap (IRS).
