The change-making problem addresses the question of finding the minimum number of coins (of certain denominations) that add up to a given amount of money. It is a special case of the integer knapsack problem, and has applications wider than just currency.
It is also the most common variation of the coin change problem, a general case of partition in which, given the available denominations of an infinite set of coins, the objective is to find out the number of possible ways of making a change for a specific amount of money, without considering the order of the coins.
It is weakly NP-hard, but may be solved optimally in pseudo-polynomial time by dynamic programming. [1] [2]
Coin values can be modeled by a set of n distinct positive integer values (whole numbers), arranged in increasing order as w1 through wn. The problem is: given an amount W, also a positive integer, to find a set of non-negative (positive or zero) integers {x1, x2, ..., xn}, with each xj representing how often the coin with value wj is used, which minimize the total number of coins f(W)
subject to
An application of change-making problem can be found in computing the ways one can make a nine dart finish in a game of darts.
Another application is computing the possible atomic (or isotopic) composition of a given mass/charge peak in mass spectrometry.
A classic dynamic programming strategy works upward by finding the combinations of all smaller values that would sum to the current threshold. [3] Thus, at each threshold, all previous thresholds are potentially considered to work upward to the goal amount W. For this reason, this dynamic programming approach requires a number of steps that is O(nW), where n is the number of types of coins.
The following is a dynamic programming implementation (with Python 3) which uses a matrix to keep track of the optimal solutions to sub-problems, and returns the minimum number of coins, or "Infinity" if there is no way to make change with the coins given. A second matrix may be used to obtain the set of coins for the optimal solution.
def_get_change_making_matrix(set_of_coins,r:int):m=[[0for_inrange(r+1)]for_inrange(len(set_of_coins)+1)]foriinrange(1,r+1):m[0][i]=float('inf')# By default there is no way of making changereturnmdefchange_making(coins,n:int):"""This function assumes that all coins are available infinitely. n is the number to obtain with the fewest coins. coins is a list or tuple with the available denominations. """m=_get_change_making_matrix(coins,n)forc,coininenumerate(coins,1):forrinrange(1,n+1):# Just use the coinifcoin==r:m[c][r]=1# coin cannot be included.# Use the previous solution for making r,# excluding coinelifcoin>r:m[c][r]=m[c-1][r]# coin can be used.# Decide which one of the following solutions is the best:# 1. Using the previous solution for making r (without using coin).# 2. Using the previous solution for making r - coin (without# using coin) plus this 1 extra coin.else:m[c][r]=min(m[c-1][r],1+m[c][r-coin])returnm[-1][-1]The probabilistic convolution tree [4] can also be used as a more efficient dynamic programming approach. The probabilistic convolution tree merges pairs of coins to produce all amounts which can be created by that pair of coins (with neither coin present, only the first coin present, only the second coin present, and both coins present), and then subsequently merging pairs of these merged outcomes in the same manner. This process is repeated until the final two collections of outcomes are merged into one, leading to a balanced binary tree with W log(W) such merge operations. Furthermore, by discretizing the coin values, each of these merge operations can be performed via convolution, which can often be performed more efficiently with the fast Fourier transform (FFT). In this manner, the probabilistic convolution tree may be used to achieve a solution in sub-quadratic number of steps: each convolution can be performed in n log(n), and the initial (more numerous) merge operations use a smaller n, while the later (less numerous) operations require n on the order of W.
The probabilistic convolution tree-based dynamic programming method also efficiently solves the probabilistic generalization of the change-making problem, where uncertainty or fuzziness in the goal amount W makes it a discrete distribution rather than a fixed quantity, where the value of each coin is likewise permitted to be fuzzy (for instance, when an exchange rate is considered), and where different coins may be used with particular frequencies.
For many real-world coin systems, such as those used in the US and many other countries, a greedy algorithm of picking the largest denomination of coin which is not greater than the remaining amount to be made will produce the optimal result. This is not the case for arbitrary coin systems or even some real world systems, though. For instance, if we consider the old (now withdrawn) Indian coin denominations of 5, 10, 20 and 25 paise, then to make 40 paise, the greedy algorithm would choose three coins (25, 10, 5) whereas the optimal solution is two coins (20, 20). Another example is attempting to make 40 US cents without nickels (denomination 25, 10, 1) with similar result — the greedy chooses seven coins (25, 10, and 5 × 1), but the optimal is four (4 × 10). A coin system is called "canonical" if the greedy algorithm always solves its change-making problem optimally. It is possible to test whether a coin system is canonical in polynomial time. [5]
The "optimal denomination problem" [6] is a problem for people who design entirely new currencies. It asks what denominations should be chosen for the coins in order to minimize the average cost of making change, that is, the average number of coins needed to make change. The version of this problem assumed that the people making change will use the minimum number of coins (from the denominations available). One variation of this problem assumes that the people making change will use the "greedy algorithm" for making change, even when that requires more than the minimum number of coins. Most current currencies use a 1-2-5 series, but some other set of denominations would require fewer denominations of coins or a smaller average number of coins to make change or both.
In mathematics and computer science, an algorithm is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use conditionals to divert the code execution through various routes and deduce valid inferences, achieving automation eventually. Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus".
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".
The knapsack problem is the following problem in combinatorial optimization:
The travelling salesperson problem, also known as travelling salesman problem (TSP), asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.
The subset sum problem (SSP) is a decision problem in computer science. In its most general formulation, there is a multiset of integers and a target-sum , and the question is to decide whether any subset of the integers sum to precisely . The problem is known to be NP-hard. Moreover, some restricted variants of it are NP-complete too, for example:
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome in a mathematical model whose requirements and objective are represented by linear relationships. Linear programming is a special case of mathematical programming.
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
Dynamic programming is both a mathematical optimization method and an algorithmic paradigm. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.
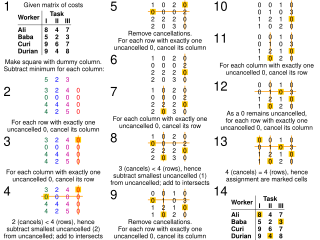
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows:
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints are linear.
Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.
In mathematics, the coin problem is a mathematical problem that asks for the largest monetary amount that cannot be obtained using only coins of specified denominations. For example, the largest amount that cannot be obtained using only coins of 3 and 5 units is 7 units. The solution to this problem for a given set of coin denominations is called the Frobenius number of the set. The Frobenius number exists as long as the set of coin denominations is setwise coprime.
In number theory and computer science, the partition problem, or number partitioning, is the task of deciding whether a given multiset S of positive integers can be partitioned into two subsets S1 and S2 such that the sum of the numbers in S1 equals the sum of the numbers in S2. Although the partition problem is NP-complete, there is a pseudo-polynomial time dynamic programming solution, and there are heuristics that solve the problem in many instances, either optimally or approximately. For this reason, it has been called "the easiest hard problem".
In mathematics, the relaxation of a (mixed) integer linear program is the problem that arises by removing the integrality constraint of each variable.
The package-merge algorithm is an O(nL)-time algorithm for finding an optimal length-limited Huffman code for a given distribution on a given alphabet of size n, where no code word is longer than L. It is a greedy algorithm, and a generalization of Huffman's original algorithm. Package-merge works by reducing the code construction problem to the binary coin collector's problem.
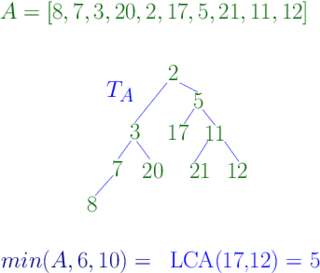
In computer science, a range minimum query (RMQ) solves the problem of finding the minimal value in a sub-array of an array of comparable objects. Range minimum queries have several use cases in computer science, such as the lowest common ancestor problem and the longest common prefix problem (LCP).
The weapon target assignment problem (WTA) is a class of combinatorial optimization problems present in the fields of optimization and operations research. It consists of finding an optimal assignment of a set of weapons of various types to a set of targets in order to maximize the total expected damage done to the opponent.
In computer science, multiway number partitioning is the problem of partitioning a multiset of numbers into a fixed number of subsets, such that the sums of the subsets are as similar as possible. It was first presented by Ronald Graham in 1969 in the context of the identical-machines scheduling problem. The problem is parametrized by a positive integer k, and called k-way number partitioning. The input to the problem is a multiset S of numbers, whose sum is k*T.