Charge-pump phase-locked loop

Last updated May 26, 2024

Charge-pump PLL CP-PLL.pdf — Charge-pump PLL

Charge-pump phase-locked loop (CP-PLL) is a modification of phase-locked loops with phase-frequency detectors and square waveform signals.^[1] A CP-PLL allows for a quick lock of the phase of the incoming signal, achieving low steady state phase error.^[2]

Phase-frequency detector (PFD)
Mathematical models of CP-PLL
Continuous time linear model of the second order CP-PLL and Gardner's conjecture
Continuous time nonlinear model of the second order CP-PLL
Discrete time nonlinear model of the second-order CP-PLL
Nonlinear models of high-order CP-PLL
References

Phase-frequency detector (PFD)

Phase-frequency detector dynamics Phase-frequency-detector.pdf — Phase-frequency detector dynamics

Phase-frequency detector (PFD) is triggered by the trailing edges of the reference (Ref) and controlled (VCO) signals. The output signal of PFD $i(t)$ can have only three states: 0, $+I_{p}$ , and $-I_{p}$ . A trailing edge of the reference signal forces the PFD to switch to a higher state, unless it is already in the state $+I_{p}$ . A trailing edge of the VCO signal forces the PFD to switch to a lower state, unless it is already in the state $-I_{p}$ . If both trailing edges happen at the same time, then the PFD switches to zero.

Mathematical models of CP-PLL

A first linear mathematical model of second-order CP-PLL was suggested by F. Gardner in 1980.^[2] A nonlinear model without the VCO overload was suggested by M. van Paemel in 1994 ^[3] and then refined by N. Kuznetsov et al. in 2019.^[4] The closed form mathematical model of CP-PLL taking into account the VCO overload is derived in.^[5]

These mathematical models of CP-PLL allow to get analytical estimations of the hold-in range (a maximum range of the input signal period such that there exists a locked state at which the VCO is not overloaded) and the pull-in range (a maximum range of the input signal period within the hold-in range such that for any initial state the CP-PLL acquires a locked state).^[6]

Continuous time linear model of the second order CP-PLL and Gardner's conjecture

Gardner's analysis is based on the following approximation:^[2] time interval on which PFD has non-zero state on each period of reference signal is

t_{p}=|\theta _{e}|/\omega _{\rm {ref}},\ \theta _{e}=\theta _{\rm {ref}}-\theta _{\rm {vco}}.

Then averaged output of charge-pump PFD is

i_{d}=I_{p}\theta _{e}/2\pi

with corresponding transfer function

I_{d}(s)=I_{p}\theta _{e}(s)/2\pi

Using filter transfer function $F(s)=R+{\frac {1}{Cs}}$ and VCO transfer function $\theta _{\rm {vco}}(s)=K_{\rm {vco}}I_{d}(s)F(s)/s$ one gets Gardner's linear approximated average model of second-order CP-PLL

{\frac {\theta _{e}(s)}{\theta _{\rm {ref}}(s)}}={\frac {2\pi s}{2\pi s+K_{\rm {vco}}I_{p}\left(R+{\frac {1}{Cs}}\right)}}.

In 1980, F. Gardner, based on the above reasoning, conjectured that transient response of practical charge-pump PLL's can be expected to be nearly the same as the response of the equivalent classical PLL^[2]^: 1856 (Gardner's conjecture on CP-PLL ^[7]). Following Gardner's results, by analogy with the Egan conjecture on the pull-in range of type 2 APLL, Amr M. Fahim conjectured in his book^[8]^: 6 that in order to have an infinite pull-in(capture) range, an active filter must be used for the loop filter in CP-PLL (Fahim-Egan's conjecture on the pull-in range of type II CP-PLL).

Continuous time nonlinear model of the second order CP-PLL

Without loss of generality it is supposed that trailing edges of the VCO and Ref signals occur when the corresponding phase reaches an integer number. Let the time instance of the first trailing edge of the Ref signal is defined as $t=0$ . The PFD state $i(0)$ is determined by the PFD initial state $i(0-)$ , the initial phase shifts of the VCO $\theta _{vco}(0)$ and Ref $\theta _{ref}(0)$ signals.

The relationship between the input current $i(t)$ and the output voltage $v_{F}(t)$ for a proportionally integrating (perfect PI) filter based on resistor and capacitor is as follows

{\begin{aligned}v_{F}(t)=v_{c}(0)+Ri(t)+{\frac {1}{C}}\int \limits _{0}^{t}i(\tau )d\tau \end{aligned}}

where $R>0$ is a resistance, $C>0$ is a capacitance, and $v_{c}(t)$ is a capacitor charge. The control signal $v_{F}(t)$ adjusts the VCO frequency:

{\begin{aligned}{\dot {\theta }}_{vco}(t)=\omega _{vco}(t)=\omega _{vco}^{\text{free}}+K_{vco}v_{F}(t),\end{aligned}}

where $\omega _{vco}^{\text{free}}$ is the VCO free-running (quiescent) frequency (i.e. for $v_{F}(t)\equiv 0$ ), $K_{vco}$ is the VCO gain (sensivity), and $\theta _{vco}(t)$ is the VCO phase. Finally, the continuous time nonlinear mathematical model of CP-PLL is as follows

{\begin{aligned}{\dot {v}}_{c}(t)={\tfrac {1}{C}}i(t),\quad {\dot {\theta }}_{vco}(t)=\omega _{vco}^{\text{free}}+K_{vco}(Ri(t)+v_{c}(t))\end{aligned}}

with the following discontinuous piece-wise constant nonlinearity

i(t)=i{\big (}i(t-),\theta _{ref}(t),\theta _{vco}(t){\big )}

and the initial conditions ${\big (}v_{c}(0),\theta _{vco}(0){\big )}$ . This model is a nonlinear, non-autonomous, discontinuous, switching system.

Discrete time nonlinear model of the second-order CP-PLL

The reference signal frequency is assumed to be constant: $\theta _{ref}(t)=\omega _{ref}t={\frac {t}{T_{ref}}},$ where $T_{ref}$ , $\omega _{ref}$ and $\theta _{ref}(t)$ are a period, frequency and a phase of the reference signal. Let $t_{0}=0$ . Denote by $t_{0}^{\rm {middle}}$ the first instant of time such that the PFD output becomes zero (if $i(0)=0$ , then $t_{0}^{\rm {middle}}=0$ ) and by $t_{1}$ the first trailing edge of the VCO or Ref. Further the corresponding increasing sequences $\{t_{k}\}$ and $\{t_{k}^{\rm {middle}}\}$ for $k=0,1,2...$ are defined. Let $t_{k}<t_{k}^{\rm {middle}}$ . Then for $t\in [t_{k},t_{k}^{\rm {middle}})$ the ${\text{sign}}(i(t))$ is a non-zero constant ( $\pm 1$ ). Denote by $\tau _{k}$ the PFD pulse width (length of the time interval, where the PFD output is a non-zero constant), multiplied by the sign of the PFD output: i.e. $\tau _{k}=(t_{k}^{\rm {middle}}-t_{k}){\text{sign}}(i(t))$ for $t\in [t_{k},t_{k}^{\rm {middle}})$ and $\tau _{k}=0$ for $t_{k}=t_{k}^{\rm {middle}}$ . If the VCO trailing edge hits before the Ref trailing edge, then $\tau _{k}<0$ and in the opposite case we have $\tau _{k}>0$ , i.e. $\tau _{k}$ shows how one signal lags behind another. Zero output of PFD $i(t)\equiv 0$ on the interval $(t_{k}^{\rm {middle}},t_{k+1})$ : $v_{F}(t)\equiv v_{k}$ for $t\in [t_{k}^{\rm {middle}},t_{k+1})$ . The transformation of variables^[9] $(\tau _{k},v_{k})$ to $p_{k}={\frac {\tau _{k}}{T_{\rm {ref}}}},u_{k}=T_{\rm {ref}}(\omega _{\rm {vco}}^{\text{free}}+K_{\rm {vco}}v_{k})-1,$ allows to reduce the number of parameters to two: $\alpha =K_{\rm {vco}}I_{p}T_{\rm {ref}}R,\beta ={\frac {K_{\rm {vco}}I_{p}T_{\rm {ref}}^{2}}{2C}}.$ Here $p_{k}$ is a normalized phase shift and $u_{k}+1$ is a ratio of the VCO frequency $\omega _{\rm {vco}}^{\text{free}}+K_{\rm {vco}}v_{k}$ to the reference frequency ${\frac {1}{T_{\rm {ref}}}}$ . Finally, the discrete-time model of second order CP-PLL without the VCO overload^[4]^[6]

{\begin{aligned}&u_{k+1}=u_{k}+2\beta p_{k+1},\\&p_{k+1}={\begin{cases}{\frac {-(u_{k}+\alpha +1)+{\sqrt {(u_{k}+\alpha +1)^{2}-4\beta c_{k}}}}{2\beta }},\quad {\text{ for }}p_{k}\geq 0,\quad c_{k}\leq 0,\\{\frac {1}{u_{k}+1}}-1+(p_{k}{\text{ mod }}1),\quad {\text{ for }}p_{k}\geq 0,\quad c_{k}>0,\\l_{k}-1,\quad {\text{ for }}p_{k}<0,\quad l_{k}\leq 1,\\{\frac {-(u_{k}+\alpha +1)+{\sqrt {(u_{k}+\alpha +1)^{2}-4\beta d_{k}}}}{2\beta }},\quad {\text{ for }}p_{k}<0,\quad l_{k}>1,\end{cases}}\end{aligned}}

where

{\begin{aligned}c_{k}=(1-(p_{k}{\text{ mod }}1))(u_{k}+1)-1,S_{l_{k}}=-(u_{k}-\alpha +1)p_{k}+\beta p_{k}^{2},l_{k}={\frac {1-(S_{l_{k}}{\text{ mod }}1)}{u_{k}+1}},d_{k}=(S_{l_{k}}{\text{ mod }}1)+u_{k}.\end{aligned}}

This discrete-time model has the only one steady state at $(u_{k}=0,p_{k}=0)$ and allows to estimate the hold-in and pull-in ranges.^[6]

If the VCO is overloaded, i.e. ${\dot {\theta }}_{\rm {vco}}(t)$ is zero, or what is the same: $(p_{k}>0,u_{k}<2\beta p_{k}-1)$ or $(p_{k}<0,u_{k}<\alpha -1)$ , then the additional cases of the CP-PLL dynamics have to be taken into account.^[5] For any parameters the VCO overload may occur for sufficiently large frequency difference between the VCO and reference signals. In practice the VCO overload should be avoided.

Nonlinear models of high-order CP-PLL

Derivation of nonlinear mathematical models of high-order CP-PLL leads to transcendental phase equations that cannot be solved analytically and require numerical approaches like the classical fixed-point method or the Newton-Raphson approach.^[10]

Related Research Articles

A Costas loop is a phase-locked loop (PLL) based circuit which is used for carrier frequency recovery from suppressed-carrier modulation signals and phase modulation signals. It was invented by John P. Costas at General Electric in the 1950s. Its invention was described as having had "a profound effect on modern digital communications". The primary application of Costas loops is in wireless receivers. Its advantage over other PLL-based detectors is that at small deviations the Costas loop error voltage is $as compared to . This translates to double the sensitivity and also makes the Costas loop uniquely suited for tracking Doppler-shifted carriers, especially in OFDM and GPS receivers.$

A phase-locked loop or phase lock loop (PLL) is a control system that generates an output signal whose phase is fixed relative to the phase of an input signal. Keeping the input and output phase in lockstep also implies keeping the input and output frequencies the same, thus a phase-locked loop can also track an input frequency. And by incorporating a frequency divider, a PLL can generate a stable frequency that is a multiple of the input frequency.

<span class="mw-page-title-main">Bremsstrahlung</span> Electromagnetic radiation due to deceleration of charged particles

In particle physics, bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis.

In optics, a Fabry–Pérot interferometer (FPI) or etalon is an optical cavity made from two parallel reflecting surfaces. Optical waves can pass through the optical cavity only when they are in resonance with it. It is named after Charles Fabry and Alfred Perot, who developed the instrument in 1899. Etalon is from the French étalon, meaning "measuring gauge" or "standard".

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics.

In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate expectations, covariances using differentiation based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. Sometimes loosely referred to as "the" exponential family, this class of distributions is distinct because they all possess a variety of desirable properties, most importantly the existence of a sufficient statistic.

In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M. The analogous solution for a charged, rotating body is given by the Kerr–Newman metric.

The Kerr–Newman metric is the most general asymptotically flat and stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged and rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions; that is, it is a solution to the Einstein–Maxwell equations that account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.

For most numbered asteroids, almost nothing is known apart from a few physical parameters and orbital elements. Some physical characteristics can only be estimated. The physical data is determined by making certain standard assumptions.

A pendulum is a body suspended from a fixed support so that it swings freely back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back towards the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.

Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.

In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.

The direct-quadrature-zerotransformation or zero-direct-quadraturetransformation is a tensor that rotates the reference frame of a three-element vector or a three-by-three element matrix in an effort to simplify analysis. The DQZ transform is the product of the Clarke transform and the Park transform, first proposed in 1929 by Robert H. Park.

A phase detector characteristic is a function of phase difference describing the output of the phase detector.

Curvilinear coordinates can be formulated in tensor calculus, with important applications in physics and engineering, particularly for describing transportation of physical quantities and deformation of matter in fluid mechanics and continuum mechanics.

The terms hold-in range, pull-in range, and lock-in range are widely used by engineers for the concepts of frequency deviation ranges within which phase-locked loop-based circuits can achieve lock under various additional conditions.

The Peierls substitution method, named after the original work by Rudolf Peierls is a widely employed approximation for describing tightly-bound electrons in the presence of a slowly varying magnetic vector potential.

The quantum Fisher information is a central quantity in quantum metrology and is the quantum analogue of the classical Fisher information. It is one of the central quantities used to qualify the utility of an input state, especially in Mach–Zehnder interferometer-based phase or parameter estimation. It is shown that the quantum Fisher information can also be a sensitive probe of a quantum phase transition. The quantum Fisher information $of a state with respect to the observable is defined as$

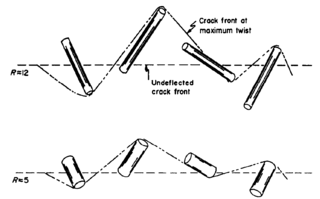
The Faber–Evans model for crack deflection, is a fracture mechanics-based approach to predict the increase in toughness in two-phase ceramic materials due to crack deflection. The effect is named after Katherine Faber and her mentor, Anthony G. Evans, who introduced the model in 1983. The Faber–Evans model is a principal strategy for tempering brittleness and creating effective ductility.

References

↑ USA US3714463A,Jon M. Laune,"Digital frequency and/or phase detector charge pump",published 1973-01-30
1 2 3 4 F. Gardner (1980). "Charge-pump phase-lock loops". IEEE Transactions on Communications. 28 (11): 1849–1858. Bibcode:1980ITCom..28.1849G. doi:10.1109/TCOM.1980.1094619.
↑ M. van Paemel (1994). "Analysis of a charge-pump pll: A new model". IEEE Transactions on Communications. 42 (7): 2490–2498. doi:10.1109/26.297861.
1 2 N. Kuznetsov, M. Yuldashev, R. Yuldashev, M. Blagov, E. Kudryashova, O. Kuznetsova, and T. Mokaev (2019). "Comments on van Paemel's mathematical model of charge-pump phase-locked loop" (PDF). Differential Equations and Control Processes. 1: 109–120.{{cite journal}}: CS1 maint: multiple names: authors list (link)
1 2 N. Kuznetsov, M. Yuldashev, R. Yuldashev, M. Blagov, E. Kudryashova, O. Kuznetsova, T. Mokaev (2020). "Charge pump phase-locked loop with phase-frequency detector: closed form mathematical model". 1901 (1468). arXiv: 1901.01468 .{{cite journal}}: Cite journal requires |journal= (help)CS1 maint: multiple names: authors list (link)
1 2 3 N.V. Kuznetsov, A.S. Matveev, M.V. Yuldashev, R.V. Yuldashev (2020). "Nonlinear analysis of charge-pump phase-locked loop: the hold-in and pull-in ranges". IFAC World Congress. arXiv: 2005.00864 .{{cite journal}}: CS1 maint: multiple names: authors list (link)
↑ Kuznetsov, N.V.; Matveev, A.S.; Yuldashev, M.V.; Yuldashev, R.V. (2021). "Nonlinear Analysis of Charge-Pump Phase-Locked Loop: The Hold-In and Pull-In Ranges". IEEE Transactions on Circuits and Systems I: Regular Papers. 68 (10): 4049–4061. arXiv: 2005.00864 . doi: 10.1109/TCSI.2021.3101529 .
↑ Fahim, Amr M. (2005). Clock Generators for SOC Processors: Circuits and Architecture. Boston-Dordrecht-London: Kluwer Academic Publishers.
↑ P. Curran, C. Bi, and O. Feely (2013). "Dynamics of charge-pump phase-locked loops". International Journal of Circuit Theory and Applications . 41 (11): 1109–1135. doi: 10.1002/cta.1814 . S2CID 3792988.{{cite journal}}: CS1 maint: multiple names: authors list (link)
↑ C. Hedayat, A. Hachem, Y. Leduc, and G. Benbassat (1999). "Modeling and characterization of the 3rd order charge-pump PLL: a fully event-driven approach". Analog Integrated Circuits and Signal Processing. 19 (1): 25–45. doi:10.1023/A:1008326315191. S2CID 58204942.{{cite journal}}: CS1 maint: multiple names: authors list (link)

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] USA US3714463A,Jon M. Laune,"Digital frequency and/or phase detector charge pump",published 1973-01-30

[Gardner-1980-2] 1 2 3 4 F. Gardner (1980). "Charge-pump phase-lock loops". IEEE Transactions on Communications. 28 (11): 1849–1858. Bibcode:1980ITCom..28.1849G. doi:10.1109/TCOM.1980.1094619.

[Paemel-1984-3] M. van Paemel (1994). "Analysis of a charge-pump pll: A new model". IEEE Transactions on Communications. 42 (7): 2490–2498. doi:10.1109/26.297861.

[Kuznetsov-2019-JDECP-4] 1 2 N. Kuznetsov, M. Yuldashev, R. Yuldashev, M. Blagov, E. Kudryashova, O. Kuznetsova, and T. Mokaev (2019). "Comments on van Paemel's mathematical model of charge-pump phase-locked loop" (PDF). Differential Equations and Control Processes. 1: 109–120.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[KuznetsovYYBKKM-2020-5] 1 2 N. Kuznetsov, M. Yuldashev, R. Yuldashev, M. Blagov, E. Kudryashova, O. Kuznetsova, T. Mokaev (2020). "Charge pump phase-locked loop with phase-frequency detector: closed form mathematical model". 1901 (1468). arXiv: 1901.01468 .{{cite journal}}: Cite journal requires |journal= (help)CS1 maint: multiple names: authors list (link)

[KuznetsovMYY-2020-6] 1 2 3 N.V. Kuznetsov, A.S. Matveev, M.V. Yuldashev, R.V. Yuldashev (2020). "Nonlinear analysis of charge-pump phase-locked loop: the hold-in and pull-in ranges". IFAC World Congress. arXiv: 2005.00864 .{{cite journal}}: CS1 maint: multiple names: authors list (link)

[2021-TCAS-KuznetsovMYY-7] Kuznetsov, N.V.; Matveev, A.S.; Yuldashev, M.V.; Yuldashev, R.V. (2021). "Nonlinear Analysis of Charge-Pump Phase-Locked Loop: The Hold-In and Pull-In Ranges". IEEE Transactions on Circuits and Systems I: Regular Papers. 68 (10): 4049–4061. arXiv: 2005.00864 . doi: 10.1109/TCSI.2021.3101529 .

[2005-Fahim-8] Fahim, Amr M. (2005). Clock Generators for SOC Processors: Circuits and Architecture. Boston-Dordrecht-London: Kluwer Academic Publishers.

[9] P. Curran, C. Bi, and O. Feely (2013). "Dynamics of charge-pump phase-locked loops". International Journal of Circuit Theory and Applications . 41 (11): 1109–1135. doi: 10.1002/cta.1814 . S2CID 3792988.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[10] C. Hedayat, A. Hachem, Y. Leduc, and G. Benbassat (1999). "Modeling and characterization of the 3rd order charge-pump PLL: a fully event-driven approach". Analog Integrated Circuits and Signal Processing. 19 (1): 25–45. doi:10.1023/A:1008326315191. S2CID 58204942.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]