Circumcenter of mass

Last updated October 21, 2022

In geometry, the circumcenter of mass is a center associated with a polygon which shares many of the properties of the center of mass. More generally, the circumcenter of mass may be defined for simplicial polytopes and also in the spherical and hyperbolic geometries.

Definition in the plane

Let $P$ be an oriented polygon (with vertices counted countercyclically) in the plane with vertices $V_{1},V_{2},\ldots ,V_{n}$ and let $O$ be an arbitrary point not lying on the sides (or their extensions). Consider the triangulation of $P$ by the oriented triangles $OV_{i}V_{i+1}$ (the index $i$ is viewed modulo $n$ ). Associate with each of these triangles its circumcenter $C_{i}$ with weight equal to its oriented area (positive if its sequence of vertices is countercyclical; negative otherwise). The circumcenter of mass of $P$ is the center of mass of these weighted circumcenters. The result is independent of the choice of point $O$ .^[3]

Circumcenter of mass of a polygon. PolyCCM.svg — Circumcenter of mass of a polygon.

Properties

In the special case when the polygon is cyclic, the circumcenter of mass coincides with the circumcenter.

The circumcenter of mass satisfies an analog of Archimedes' Lemma, which states that if a polygon is decomposed into two smaller polygons, then the circumcenter of mass of that polygon is a weighted sum of the circumcenters of mass of the two smaller polygons. As a consequence, any triangulation with nondegenerate triangles may be used to define the circumcenter of mass.

For an equilateral polygon, the circumcenter of mass and center of mass coincide. More generally, the circumcenter of mass and center of mass coincide for a simplicial polytope for which each face has the sum of squares of its edges a constant.^[4]

The circumcenter of mass is invariant under the operation of "recutting" of polygons.^[5] and the discrete bicycle (Darboux) transformation; in other words, the image of a polygon under these operations has the same circumcenter of mass as the original polygon. The generalized Euler line makes other appearances in the theory of integrable systems.^[6]

Let $V_{i}=(x_{i},y_{i})$ be the vertices of $P$ and let $A$ denote its area. The circumcenter of mass $CCM(P)$ of the polygon $P$ is given by the formula

CCM(P)={\frac {1}{4A}}(\sum _{i=0}^{n-1}-y_{i}y_{i+1}^{2}+y_{i}^{2}y_{i+1}+x_{i}^{2}y_{i+1}-x_{i+1}^{2}y_{i},\sum _{i=0}^{n-1}-x_{i+1}y_{i}^{2}+x_{i}y_{i+1}^{2}+x_{i}x_{i+1}^{2}-x_{i}^{2}x_{i+1}).

The circumcenter of mass can be extended to smooth curves via a limiting procedure. This continuous limit coincides with the center of mass of the homogeneous lamina bounded by the curve.

Under natural assumptions, the centers of polygons which satisfy Archimedes' Lemma are precisely the points of its Euler line. In other words, the only "well-behaved" centers which satisfy Archimedes' Lemma are the affine combinations of the circumcenter of mass and center of mass.

Generalized Euler line

The circumcenter of mass allows an Euler line to be defined for any polygon (and more generally, for a simplicial polytope). This generalized Euler line is defined as the affine span of the center of mass and circumcenter of mass of the polytope.

Related Research Articles

In elementary geometry, a polytope is a geometric object with flat sides (faces). It is a generalization in any number of dimensions of the three-dimensional polyhedron. Polytopes may exist in any general number of dimensions $n$ as an $n$ -dimensional polytope or $n$ -polytope. In this context, "flat sides" means that the sides of a $(k + 1)$ -polytope consist of $k$ -polytopes that may have $(k - 1)$ -polytopes in common. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope.

In geometry, a polygon is a plane figure that is described by a finite number of straight line segments connected to form a closed polygonal chain. The bounded plane region, the bounding circuit, or the two together, may be called a polygon.

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices $,, and is sometimes denoted as .$

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

<span class="mw-page-title-main">Equilateral triangle</span> Shape with three equal sides

In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

<span class="mw-page-title-main">Centroid</span> Mean ("average") position of all the points in a shape

In mathematics and physics, the centroid or geometric center of a plane figure is the arithmetic mean position of all the points in the figure. Informally, it is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin. The same definition extends to any object in n-dimensional space.

<span class="mw-page-title-main">Euler line</span> Line constructed from a triangle

In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.

<span class="mw-page-title-main">Incenter</span> Center of the inscribed circle of a triangle

In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

<span class="mw-page-title-main">Midpoint</span> Point on a line segment which is equidistant from both endpoints

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

<span class="mw-page-title-main">Concyclic points</span> Points on a common circle

In geometry, a set of points are said to be concyclic if they lie on a common circle. All concyclic points are at the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ABCD would be denoted $ABCD .$

<span class="mw-page-title-main">Convex polytope</span> Convex hull of a finite set of points in a Euclidean space

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the $-dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.$

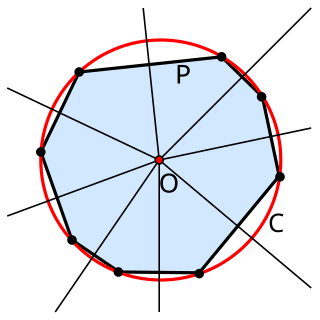
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.

In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

The medial triangle or midpoint triangle of a triangle ABC is the triangle with vertices at the midpoints of the triangle's sides AB, AC and BC. It is the n=3 case of the midpoint polygon of a polygon with n sides. The medial triangle is not the same thing as the median triangle, which is the triangle whose sides have the same lengths as the medians of ABC.

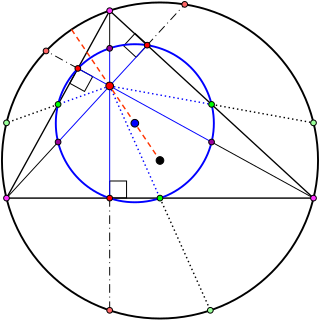
In geometry, the nine-point center is a triangle center, a point defined from a given triangle in a way that does not depend on the placement or scale of the triangle. It is so called because it is the center of the nine-point circle, a circle that passes through nine significant points of the triangle: the midpoints of the three edges, the feet of the three altitudes, and the points halfway between the orthocenter and each of the three vertices. The nine-point center is listed as point X(5) in Clark Kimberling's Encyclopedia of Triangle Centers.

In geometry, a vertex, often denoted by letters such as $,,,, is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.$

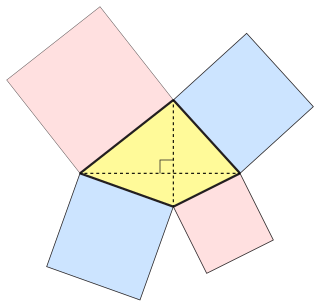
In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal (perpendicular) to each other.

In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.

References

↑ Myakishev, Alexei (2006), "On Two Remarkable Lines Related to a Quadrilateral" (PDF), Forum Geometricorum, 6: 289–295.
↑ de Villiers, Michael (2014), "Quasi-circumcenters and a generalization of the quasi-Euler line to a hexagon" (PDF), Forum Geometricorum, 14: 233–236
↑ Tabachnikov, Serge; Tsukerman, Emmanuel (May 2014), "Circumcenter of Mass and Generalized Euler Line", Discrete and Computational Geometry , 51 (4): 815–836, arXiv: 1301.0496 , doi:10.1007/s00454-014-9597-2, S2CID 12307207
↑ Akopyan, Arseniy (May 2014), "Some Remarks on the Circumcenter of Mass", Discrete and Computational Geometry , 51 (4): 837–841, arXiv: 1512.08655 , doi:10.1007/s00454-014-9596-3, S2CID 3464833
↑ Adler, V. (1993), "Cutting of polygons", Funct. Anal. Appl., 27 (2): 141–143, doi:10.1007/BF01085984, S2CID 122179363
↑ Schief, W. K. (2014), "Integrable structure in discrete shell membrane theory", Proceedings of the Royal Society of London A, 470 (2165): 22, doi:10.1098/rspa.2013.0757, PMC 3973394 , PMID 24808755

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Myakishev, Alexei (2006), "On Two Remarkable Lines Related to a Quadrilateral" (PDF), Forum Geometricorum, 6: 289–295.

[2] Villiers, Michael (2014), "Quasi-circumcenters and a generalization of the quasi-Euler line to a hexagon" (PDF), Forum Geometricorum, 14: 233–236

[3] Tabachnikov, Serge; Tsukerman, Emmanuel (May 2014), "Circumcenter of Mass and Generalized Euler Line", Discrete and Computational Geometry , 51 (4): 815–836, arXiv: 1301.0496 , doi:10.1007/s00454-014-9597-2, S2CID 12307207

[4] Akopyan, Arseniy (May 2014), "Some Remarks on the Circumcenter of Mass", Discrete and Computational Geometry , 51 (4): 837–841, arXiv: 1512.08655 , doi:10.1007/s00454-014-9596-3, S2CID 3464833

[5] Adler, V. (1993), "Cutting of polygons", Funct. Anal. Appl., 27 (2): 141–143, doi:10.1007/BF01085984, S2CID 122179363

[6] Schief, W. K. (2014), "Integrable structure in discrete shell membrane theory", Proceedings of the Royal Society of London A, 470 (2165): 22, doi:10.1098/rspa.2013.0757, PMC 3973394 , PMID 24808755

[1]

[2]

[3]

[4]

[5]

[6]