In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.

In logic, disjunction, also known as logical disjunction or logical or or logical addition or inclusive disjunction, is a logical connective typically notated as and read aloud as "or". For instance, the English language sentence "it is sunny or it is warm" can be represented in logic using the disjunctive formula , assuming that abbreviates "it is sunny" and abbreviates "it is warm".
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.
Many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition. Classical two-valued logic may be extended to n-valued logic for n greater than 2. Those most popular in the literature are three-valued, four-valued, nine-valued, the finite-valued with more than three values, and the infinite-valued (infinitely-many-valued), such as fuzzy logic and probability logic.
In boolean logic, a disjunctive normal form (DNF) is a canonical normal form of a logical formula consisting of a disjunction of conjunctions; it can also be described as an OR of ANDs, a sum of products, or — in philosophical logic — a cluster concept. As a normal form, it is useful in automated theorem proving.
In Boolean logic, a formula is in conjunctive normal form (CNF) or clausal normal form if it is a conjunction of one or more clauses, where a clause is a disjunction of literals; otherwise put, it is a product of sums or an AND of ORs. As a canonical normal form, it is useful in automated theorem proving and circuit theory.

In Boolean logic, logical NOR, non-disjunction, or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form (p NOR q) is true precisely when neither p nor q is true—i.e. when both p and q are false. It is logically equivalent to and , where the symbol signifies logical negation, signifies OR, and signifies AND.
In mathematical logic and logic programming, a Horn clause is a logical formula of a particular rule-like form that gives it useful properties for use in logic programming, formal specification, universal algebra and model theory. Horn clauses are named for the logician Alfred Horn, who first pointed out their significance in 1951.

In proof theory, the semantic tableau (; plural: tableaux, also called an analytic tableau, truth tree, or simply tree, is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic. An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics.
In Boolean algebra, the algebraic normal form (ANF), ring sum normal form, Zhegalkin normal form, or Reed–Muller expansion is a way of writing propositional logic formulas in one of three subforms:
In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable or not. Horn-satisfiability and Horn clauses are named after Alfred Horn.
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation-complete theorem-proving technique for sentences in propositional logic and first-order logic. For propositional logic, systematically applying the resolution rule acts as a decision procedure for formula unsatisfiability, solving the Boolean satisfiability problem. For first-order logic, resolution can be used as the basis for a semi-algorithm for the unsatisfiability problem of first-order logic, providing a more practical method than one following from Gödel's completeness theorem.
The concept of a stable model, or answer set, is used to define a declarative semantics for logic programs with negation as failure. This is one of several standard approaches to the meaning of negation in logic programming, along with program completion and the well-founded semantics. The stable model semantics is the basis of answer set programming.
Constraint logic programming is a form of constraint programming, in which logic programming is extended to include concepts from constraint satisfaction. A constraint logic program is a logic program that contains constraints in the body of clauses. An example of a clause including a constraint is A(X,Y):-X+Y>0,B(X),C(Y). In this clause, X+Y>0 is a constraint; A(X,Y), B(X), and C(Y) are literals as in regular logic programming. This clause states one condition under which the statement A(X,Y) holds: X+Y is greater than zero and both B(X) and C(Y) are true.
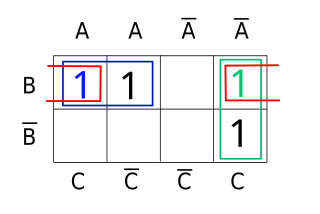
In Boolean algebra, the consensus theorem or rule of consensus is the identity:
SLD resolution is the basic inference rule used in logic programming. It is a refinement of resolution, which is both sound and refutation complete for Horn clauses.
In mathematical logic, two formulae are equisatisfiable if the first formula is satisfiable whenever the second is and vice versa; in other words, either both formulae are satisfiable or both are not. Equisatisfiable formulae may disagree, however, for a particular choice of variables. As a result, equisatisfiability is different from logical equivalence, as two equivalent formulae always have the same models. Whereas within equisatisfiable formulae, only the primitive proposition the formula imposes is valued.
In mathematics, a read-once function is a special type of Boolean function that can be described by a Boolean expression in which each variable appears only once.
ProbLog is a probabilistic logic programming language that extends Prolog with probabilities. It minimally extends Prolog by adding the notion of a probabilistic fact, which combines the idea of logical atoms and random variables. Similarly to Prolog, ProbLog can query an atom. While Prolog returns the truth value of the queried atom, ProbLog returns the probability of it being true.
Logic programming is a programming paradigm that includes languages based on formal logic, including Datalog and Prolog. This article describes the syntax and semantics of the purely declarative subset of these languages. Confusingly, the name "logic programming" also refers to a specific programming language that roughly corresponds to the declarative subset of Prolog. Unfortunately, the term must be used in both senses in this article.














