
The exponential function is a mathematical function denoted by or . Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the operation of taking powers of a number, but various modern definitions allow it to be rigorously extended to all real arguments , including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to consider the exponential function to be "the most important function in mathematics".

In mathematics, the logarithm is the inverse function to exponentiation. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 103, the logarithm base 10 of 1000 is 3, or log10 (1000) = 3. The logarithm of x to base b is denoted as logb (x), or without parentheses, logb x, or even without the explicit base, log x, when no confusion is possible, or when the base does not matter such as in big O notation.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.
An order of magnitude is an approximation of the logarithm of a value relative to some contextually understood reference value, usually 10, interpreted as the base of the logarithm and the representative of values of magnitude one. Logarithmic distributions are common in nature and considering the order of magnitude of values sampled from such a distribution can be more intuitive. When the reference value is 10, the order of magnitude can be understood as the number of digits in the base-10 representation of the value. Similarly, if the reference value is one of some powers of 2, since computers store data in a binary format, the magnitude can be understood in terms of the amount of computer memory needed to store that value.

A slide rule is a hand-operated mechanical calculator consisting of slidable rulers for evaluating mathematical operations such as multiplication, division, exponents, roots, logarithms, and trigonometry. It is one of the simplest analog computers.

The neper is a logarithmic unit for ratios of measurements of physical field and power quantities, such as gain and loss of electronic signals. The unit's name is derived from the name of John Napier, the inventor of logarithms. As is the case for the decibel and bel, the neper is a unit defined in the international standard ISO 80000. It is not part of the International System of Units (SI), but is accepted for use alongside the SI.
In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy-channel coding theorem to the archetypal case of a continuous-time analog communications channel subject to Gaussian noise. The theorem establishes Shannon's channel capacity for such a communication link, a bound on the maximum amount of error-free information per time unit that can be transmitted with a specified bandwidth in the presence of the noise interference, assuming that the signal power is bounded, and that the Gaussian noise process is characterized by a known power or power spectral density. The law is named after Claude Shannon and Ralph Hartley.
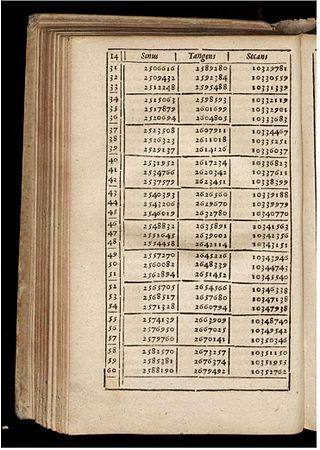
Mathematical tables are lists of numbers showing the results of a calculation with varying arguments. Trigonometric tables were used in ancient Greece and India for applications to astronomy and celestial navigation, and continued to be widely used until electronic calculators became cheap and plentiful, in order to simplify and drastically speed up computation. Tables of logarithms and trigonometric functions were common in math and science textbooks, and specialized tables were published for numerous applications.

In mathematics, the binary logarithm is the power to which the number 2 must be raised to obtain the value n. That is, for any real number x,

In mathematics, an identity is an equality relating one mathematical expression A to another mathematical expression B, such that A and B produce the same value for all values of the variables within a certain range of validity. In other words, A = B is an identity if A and B define the same functions, and an identity is an equality between functions that are differently defined. For example, and are identities. Identities are sometimes indicated by the triple bar symbol ≡ instead of =, the equals sign. Formally, an identity is a universally quantified equality.
The significand is the first (left) part of a number in scientific notation or in floating-point representation, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.

In mathematics, tetration is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though and the left-exponent xb are common.

The term Napierian logarithm or Naperian logarithm, named after John Napier, is often used to mean the natural logarithm. Napier did not introduce this natural logarithmic function, although it is named after him. However, if it is taken to mean the "logarithms" as originally produced by Napier, it is a function given by :

One decade is a unit for measuring ratios on a logarithmic scale, with one decade corresponding to a ratio of 10 between two numbers.
An overline, overscore, or overbar, is a typographical feature of a horizontal line drawn immediately above the text. In old mathematical notation, an overline was called a vinculum, a notation for grouping symbols which is expressed in modern notation by parentheses, though it persists for symbols under a radical sign. The original use in Ancient Greek was to indicate compositions of Greek letters as Greek numerals. In Latin, it indicates Roman numerals multiplied by a thousand and it forms medieval abbreviations (sigla). Marking one or more words with a continuous line above the characters is sometimes called overstriking, though overstriking generally refers to printing one character on top of an already-printed character.

The history of logarithms is the story of a correspondence between multiplication on the positive real numbers and addition on the real number line that was formalized in seventeenth century Europe and was widely used to simplify calculation until the advent of the digital computer. The Napierian logarithms were published first in 1614. E. W. Hobson called it "one of the very greatest scientific discoveries that the world has seen." Henry Briggs introduced common logarithms, which were easier to use. Tables of logarithms were published in many forms over four centuries. The idea of logarithms was also used to construct the slide rule, which became ubiquitous in science and engineering until the 1970s. A breakthrough generating the natural logarithm was the result of a search for an expression of area against a rectangular hyperbola, and required the assimilation of a new function into standard mathematics.

Casio fx-3650P is a programmable scientific calculator manufactured by Casio Computer Co., Ltd. It can store 12 digits for the mantissa and 2 digits for the exponent together with the expression each time when the "EXE" button is pressed. Also, the calculator can use the previous result to do calculations by pressing "Ans". It is one of the calculators approved by HKEAA to be used in public examinations in Hong Kong, such as HKDSE.

In probability and statistics, the reciprocal distribution, also known as the log-uniform distribution, is a continuous probability distribution. It is characterised by its probability density function, within the support of the distribution, being proportional to the reciprocal of the variable.
In mathematics, the set of positive real numbers, is the subset of those real numbers that are greater than zero. The non-negative real numbers, also include zero. Although the symbols and are ambiguously used for either of these, the notation or for and or for has also been widely employed, is aligned with the practice in algebra of denoting the exclusion of the zero element with a star, and should be understandable to most practicing mathematicians.





































