
In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction.
The quantum Hall effect is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values

Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The interactions among the particles of the many-body system do not need to be small. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas, and why other properties differ.

In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change i.e. a minimum in electrical resistivity with temperature. The cause of the effect was first explained by Jun Kondo, who applied third-order perturbation theory to the problem to account for scattering of s-orbital conduction electrons off d-orbital electrons localized at impurities. Kondo's calculation predicted that the scattering rate and the resulting part of the resistivity should increase logarithmically as the temperature approaches 0 K. Experiments in the 1960s by Myriam Sarachik at Bell Laboratories provided the first data that confirmed the Kondo effect. Extended to a lattice of magnetic impurities, the Kondo effect likely explains the formation of heavy fermions and Kondo insulators in intermetallic compounds, especially those involving rare earth elements such as cerium, praseodymium, and ytterbium, and actinide elements such as uranium. The Kondo effect has also been observed in quantum dot systems.
In physics, an anyon is a type of quasiparticle that occurs only in two-dimensional systems, with properties much less restricted than the two kinds of standard elementary particles, fermions and bosons. In general, the operation of exchanging two identical particles, although it may cause a global phase shift, cannot affect observables. Anyons are generally classified as abelian or non-abelian. Abelian anyons play a major role in the fractional quantum Hall effect. Non-abelian anyons have not been definitively detected, although this is an active area of research.
The fractional quantum Hall effect (FQHE) is a physical phenomenon in which the Hall conductance of 2-dimensional (2D) electrons shows precisely quantized plateaus at fractional values of . It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations have a fractional elementary charge and possibly also fractional statistics. The 1998 Nobel Prize in Physics was awarded to Robert Laughlin, Horst Störmer, and Daniel Tsui "for their discovery of a new form of quantum fluid with fractionally charged excitations" Laughlin's explanation only applies to fillings where is an odd integer. The microscopic origin of the FQHE is a major research topic in condensed matter physics.

In condensed matter physics, Hofstadter's butterfly is a graph of the spectral properties of non-interacting two-dimensional electrons in a perpendicular magnetic field in a lattice. The fractal, self-similar nature of the spectrum was discovered in the 1976 Ph.D. work of Douglas Hofstadter and is one of the early examples of modern scientific data visualization. The name reflects the fact that, as Hofstadter wrote, "the large gaps [in the graph] form a very striking pattern somewhat resembling a butterfly."

In physics, topological order is a kind of order in the zero-temperature phase of matter. Macroscopically, topological order is defined and described by robust ground state degeneracy and quantized non-Abelian geometric phases of degenerate ground states. Microscopically, topological orders correspond to patterns of long-range quantum entanglement. States with different topological orders cannot change into each other without a phase transition.
A two-dimensional electron gas (2DEG) is a scientific model in solid-state physics. It is an electron gas that is free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels for motion in the third direction, which can then be ignored for most problems. Thus the electrons appear to be a 2D sheet embedded in a 3D world. The analogous construct of holes is called a two-dimensional hole gas (2DHG), and such systems have many useful and interesting properties.
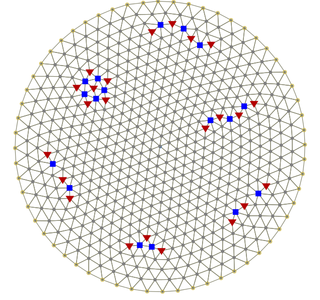
A Wigner crystal is the solid (crystalline) phase of electrons first predicted by Eugene Wigner in 1934. A gas of electrons moving in a uniform, inert, neutralizing background will crystallize and form a lattice if the electron density is less than a critical value. This is because the potential energy dominates the kinetic energy at low densities, so the detailed spatial arrangement of the electrons becomes important. To minimize the potential energy, the electrons form a bcc lattice in 3D, a triangular lattice in 2D and an evenly spaced lattice in 1D. Most experimentally observed Wigner clusters exist due to the presence of the external confinement, i.e. external potential trap. As a consequence, deviations from the b.c.c or triangular lattice are observed. A crystalline state of the 2D electron gas can also be realized by applying a sufficiently strong magnetic field. However, it is still not clear whether it is the Wigner crystallization that has led to observation of insulating behaviour in magnetotransport measurements on 2D electron systems, since other candidates are present, such as Anderson localization.
A topological quantum computer is a theoretical quantum computer proposed by Russian-American physicist Alexei Kitaev in 1997. It employs quasiparticles in two-dimensional systems, called anyons, whose world lines pass around one another to form braids in a three-dimensional spacetime. These braids form the logic gates that make up the computer. The advantage of a quantum computer based on quantum braids over using trapped quantum particles is that the former is much more stable. Small, cumulative perturbations can cause quantum states to decohere and introduce errors in the computation, but such small perturbations do not change the braids' topological properties. This is like the effort required to cut a string and reattach the ends to form a different braid, as opposed to a ball bumping into a wall.

A Majorana fermion, also referred to as a Majorana particle, is a fermion that is its own antiparticle. They were hypothesised by Ettore Majorana in 1937. The term is sometimes used in opposition to a Dirac fermion, which describes fermions that are not their own antiparticles.
In solid-state physics, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons in unfilled electron bands. Electrons are one type of fermion, and when they are found in such materials, they are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free electron model. The properties of the heavy fermion compounds often derive from the partly filled f-orbitals of rare-earth or actinide ions, which behave like localized magnetic moments. The name "heavy fermion" comes from the fact that the fermion behaves as if it has an effective mass greater than its rest mass. In the case of electrons, below a characteristic temperature (typically 10 K), the conduction electrons in these metallic compounds behave as if they had an effective mass up to 1000 times the free particle mass. This large effective mass is also reflected in a large contribution to the resistivity from electron-electron scattering via the Kadowaki–Woods ratio. Heavy fermion behavior has been found in a broad variety of states including metallic, superconducting, insulating and magnetic states. Characteristic examples are CeCu6, CeAl3, CeCu2Si2, YbAl3, UBe13 and UPt3.
The quantum spin Hall state is a state of matter proposed to exist in special, two-dimensional semiconductors that have a quantized spin-Hall conductance and a vanishing charge-Hall conductance. The quantum spin Hall state of matter is the cousin of the integer quantum Hall state, and that does not require the application of a large magnetic field. The quantum spin Hall state does not break charge conservation symmetry and spin- conservation symmetry.
In particle physics and string theory (M-theory), the ADD model, also known as the model with large extra dimensions (LED), is a model framework that attempts to solve the hierarchy problem. The model tries to explain this problem by postulating that our universe, with its four dimensions, exists on a membrane in a higher dimensional space. It is then suggested that the other forces of nature operate within this membrane and its four dimensions, while gravitons can propagate across the extra dimensions. This would explain why gravity is very weak compared to the other fundamental forces. The size of the dimensions in ADD is around the order of the TeV scale, which results in it being experimentally probeable by current colliders, unlike many exotic extra dimensional hypotheses that have the relevant size around the Planck scale.

In condensed matter physics, Luttinger's theorem is a result derived by J. M. Luttinger and J. C. Ward in 1960 that has broad implications in the field of electron transport. It arises frequently in theoretical models of correlated electrons, such as the high-temperature superconductors, and in photoemission, where a metal's Fermi surface can be directly observed.

Piers Coleman is a British-born theoretical physicist, working in the field of theoretical condensed matter physics. Coleman is Professor of Physics at Rutgers University in New Jersey and at Royal Holloway, University of London.
James (Jim) P. Eisenstein is the Frank J. Roshek Professor of Physics and Applied Physics at the physics department of California Institute of Technology.
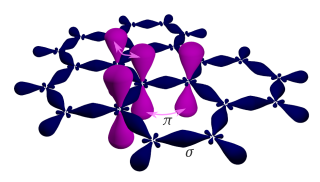
Graphene is a semimetal whose conduction and valence bands meet at the Dirac points, which are six locations in momentum space, the vertices of its hexagonal Brillouin zone, divided into two non-equivalent sets of three points. The two sets are labeled K and K'. The sets give graphene a valley degeneracy of gv = 2. By contrast, for traditional semiconductors the primary point of interest is generally Γ, where momentum is zero. Four electronic properties separate it from other condensed matter systems.
The term Dirac matter refers to a class of condensed matter systems which can be effectively described by the Dirac equation. Even though the Dirac equation itself was formulated for fermions, the quasi-particles present within Dirac matter can be of any statistics. As a consequence, Dirac matter can be distinguished in fermionic, bosonic or anyonic Dirac matter. Prominent examples of Dirac matter are Graphene, topological insulators, Dirac semimetals, Weyl semimetals, various high-temperature superconductors with -wave pairing and liquid Helium-3. The effective theory of such systems is classified by a specific choice of the Dirac mass, the Dirac velocity, the Dirac matrices and the space-time curvature. The universal treatment of the class of Dirac matter in terms of an effective theory leads to a common features with respect to the density of states, the heat capacity and impurity scattering.


















































